Evaluate ∫x−1x+1dx Solution in Tamil
The correct Answer is:B
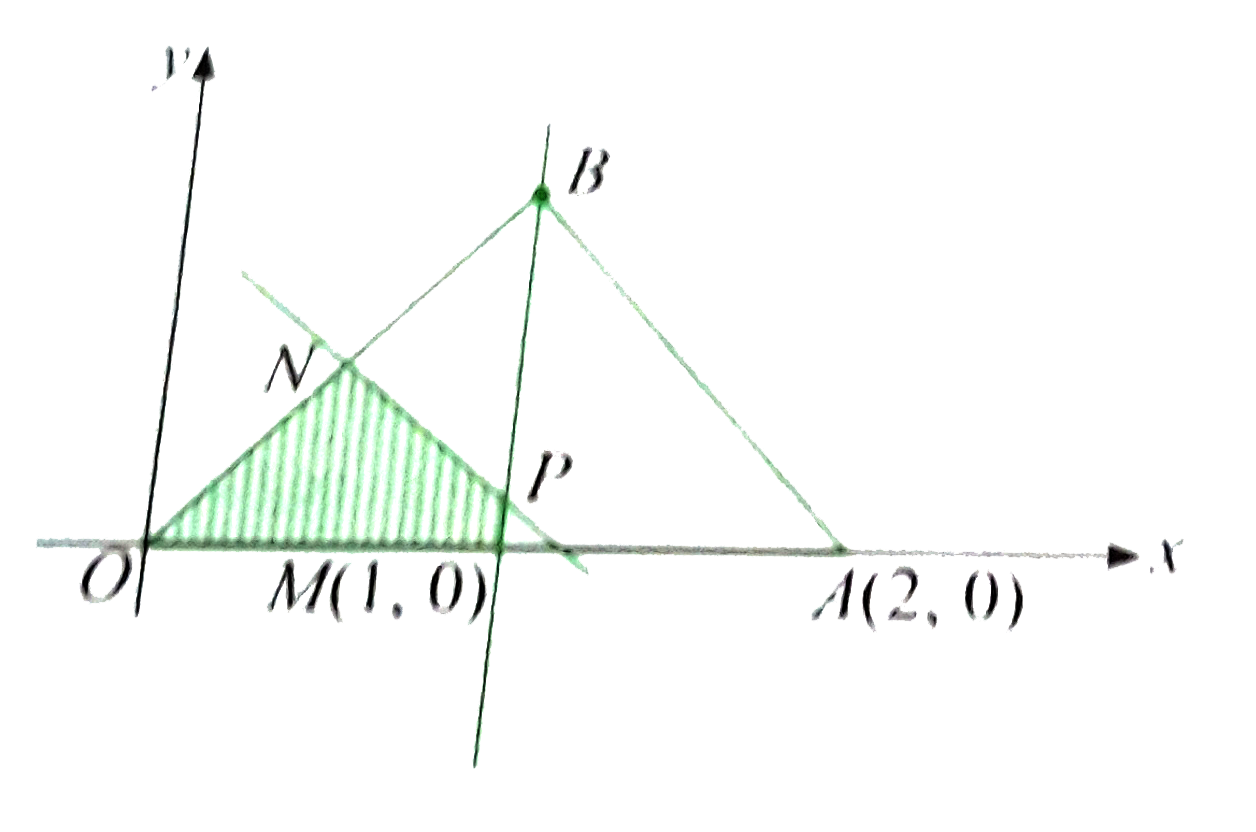
OP≤min[BP,AP]
OP≤AP(whenAP<BP)
Let OP=BP. The P lies on the perpendicular bisector of OB, For OP=AP,P lies on the perpendiuclar bisector of OA. Then, for the required condition, P lies in the region as shown in the diagram. the area of region OMPN is
12×∣∣
∣
∣
∣
∣
∣∣001011/√312√3/200∣∣
∣
∣
∣
∣
∣∣=12[1√3+√32−12√3]
=12[√32+1√3]=1√3
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Consider the triangle whose vertices are (-1,0),(5,-2) and (8,2). Find the centroid of the triangle.
View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionEvaluate: ∫log(1+1x)x(1+x)dx
View SolutionEvaluate: (i) ∫11−cosx dx (ii) ∫11−sinx dx
View SolutionEvaluate: ∫1(x−1)(x+1)(x+2) dx
View SolutionEvaluate :
(i) ∫dx1+√x (ii) ∫x+√x+1x+2dx
View SolutionEvaluate ∫(1−x1+x)dx
View SolutionFind ∫dx(x−1)(x+1)
View SolutionEvaluate: ∫1x(x−1)dx
View SolutionEvaluate: ∫log(1+1x)x(1+x)dx
View SolutionEvaluate: ∫log(1+1x)x(1+x)dx
View SolutionEvaluate: (i) ∫logxx dx (ii) ∫log(1+1x)x(1+x) dx
View Solution
