Let ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC ,G(3,2).
The coordinates of D are Solution in Tamil
(7,-4)
(5,0)
(7,4)
(-3,0)
The correct Answer is:B
Let the coordinates of D be (α,β). Then,
α+1+33=3 or α=5
and β+2+43=2 or β=0
∴D≡(5,0)
Taking A(x1,y1),B(x1,y1), and C(x3,y3), we have
x1+x22=1,
x2+x32=5,x3+x12=3
and y1+y22=5,y2+y32=0,y1+y32=4
Solving the above equations we get
A≡(−1,6),B≡(3,−2),C≡(7,2)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)4videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)12videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)13videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Consider the triangle whose vertices are (-1,0),(5,-2) and (8,2). Find the centroid of the triangle.
03:28View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
02:25View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
03:08View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC ,G(3,2).
The coordinates of D are06:00View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The height of the altitude drawn from point A is (in units)03:36View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
03:02View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
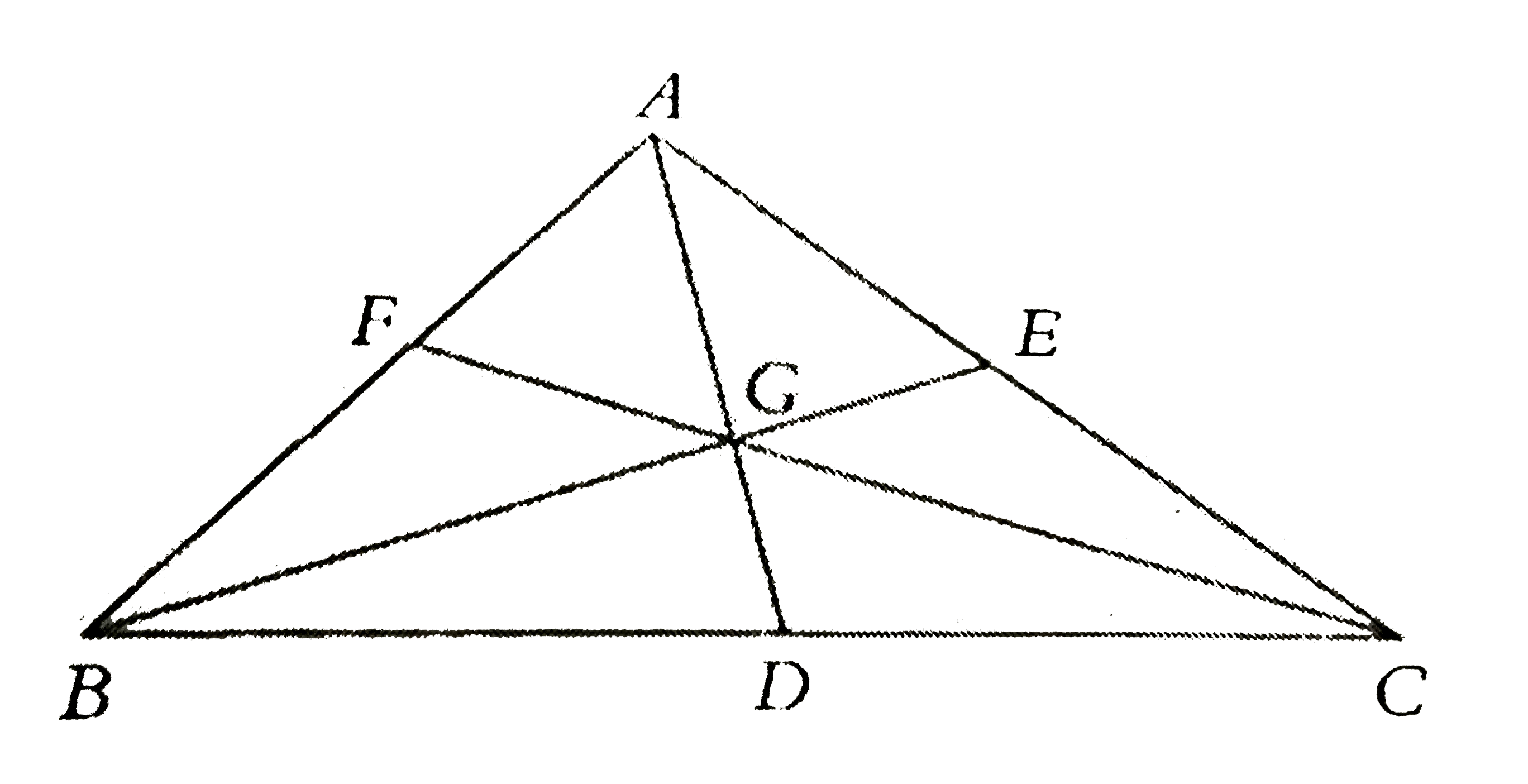 03:25View Solution
03:25View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
03:14View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are the points E(3,4) and F(1,2) respectively. The centroid of ΔABC ,G(3,2). equation of side AB is
05:22View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
04:37View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The coordinates of point D is ____________02:36View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
02:17View SolutionIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
03:26View Solution

