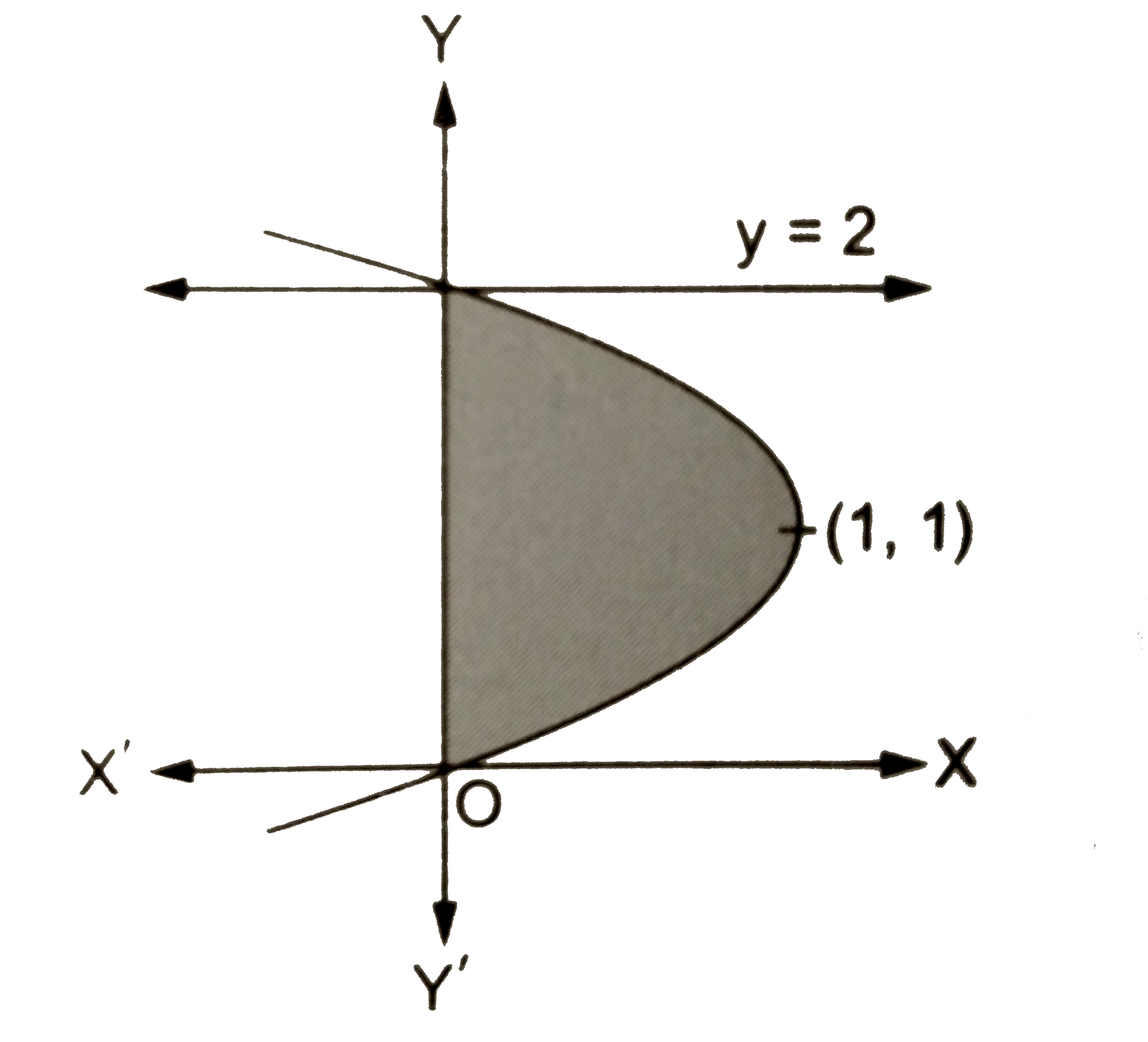
Examples: Find the area of the region bounded by the curve y2=2y−x and the y-axis.
Video Solution
Text Solution
y2=2y−x⇒y2−2y+1=−x+1
⇒(y−1)2=−(x−1)
So, the given equation represents a parabola that opens on the left, having vertex at (1,1) ,
Now , x=0⇒y2−2y⇒y2−2y=0
⇒y(y−2)=0
⇒y(y−2)=0
y=0ory=2
Thus the curve meets the y-axis at (0,0) and (0,2)
Required area =2∫0(2y−y2)dy
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the curve y=2x−x2 and x - axis is
A23 sq , unitsB43 sq,unitsC53 sq , unitsD83 sq. units
Find the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionFind the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curve y=x2 and the line y=4.
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0 and x=3.
View SolutionFind the area of the region bounded by the curves x2=8y,y=2,y=4 and the Y-axis, lying in the first quadrant.
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View Solution
