Explain how the volume of a figure is changed if each dimension is multiplied by a factor of 2.
To understand how the volume of a figure changes when each dimension is multiplied by a factor of 2, let's follow these steps:
1. Identify the Shape: Let's consider a cuboid, which has three dimensions: length (L), breadth (B), and height (H).
2. Formula for Volume: The volume (V) of a cuboid is calculated using the formula:
V=L×B×H
3. Multiply Each Dimension by 2: If we multiply each dimension by 2, the new dimensions become:
- New Length = 2L
- New Breadth = 2B
- New Height = 2H
4. Calculate the New Volume: The new volume (V') of the cuboid with the new dimensions is:
V′=(2L)×(2B)×(2H)
5. Simplify the New Volume: Now, let's simplify the expression for the new volume:
V′=2L×2B×2H=8×(L×B×H)
Thus, we can express the new volume as:
V′=8V
This means that the new volume is 8 times the original volume.
6. Conclusion: Therefore, when each dimension of a cuboid is multiplied by a factor of 2, the volume of the cuboid increases by a factor of 8.
V=L×B×H
- New Length = 2L
- New Breadth = 2B
- New Height = 2H
V′=(2L)×(2B)×(2H)
V′=2L×2B×2H=8×(L×B×H)
Thus, we can express the new volume as:
V′=8V
This means that the new volume is 8 times the original volume.
Topper's Solved these Questions
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - TRY THIS
5 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
Similar Questions
Knowledge Check
The mean of 8 numbers is 25. If each number is multiplied by 2, the new mean will be
A12.5B25C40D50The mean of 15 observation is 23. If each obsevation is multiplied 2, then new mean is .
A23B46C25D36
Explain briefly how the methods of classification changed over time
View SolutionTell whether a figure’s surface area has increased or decreased if each dimension of the figure is changed by a factor of13.
View SolutionThe reaction A+B→ products is first order in each of the reactants.
(a) How does the rate of reaction change if the concentration of A is increased by factor 3 ?
(b) What is the change in the rate of reaction if the concentration of A is halved and concentration of B is doubled ?
View SolutionThe variation of pressure with volume of the gas at different temperatures can be graphically represented as shown in figure. On the basis of this graph answer the following question.
(i) How will the volume of a gas change if its pressure is increased at constant temperature ?
(ii) At a constant pressure, how will the volume of a gas change if the temperature is increased from 200 K to 400 K ?

View SolutionExplain how the direction of exchange of gases in plants change with the time of the day.
View SolutionThe variation of pressure with volume of the gas at different temperatures can be graphically represented as shown in figure. On the basis of this graph answer the following questions.
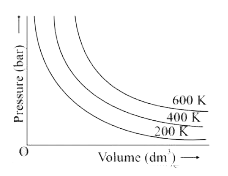
How will the volume of a gas change if its pressure is increased at constant temperature?
View Solution
