Figure shows three events A,B,C
and also the probabilities of the various intersections (for instance P(A∩B)=0.07
) determine
P(A)
(ii) P(B∩C)
(iii) P(A∩B)
(iv) P(A∩B)
(v) P(B∩C)
(vi) probability of exactly on the three events.
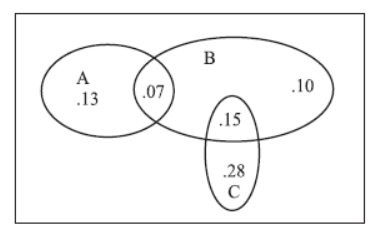
(i) P(A)=0.13+0.07=0.20.
(ii) p(B∩¯¯¯C)=p(B)−p(B∩C)=0.10+0.07+0.15end{alig≠d}
=0.10+0.07+0.15−0.15=0.17
iii) P(A∪B)=P(A)+P(B)−P(A∩B)
=0.13+0.07+0.7+0.10+0.15−0.07
=0.20+0.25=0.45.
(v) P(A∩¯¯¯B)=p(A)−P(A∩B)
=0.13+0.0.7−0.07.
=0.13
(v) P(B∩C)=0.15
(vi) 0.13+0.10+0.28=0.13+0.38=0.51.
Similar Questions
Figure shows three events A,B,C and also the probabilities of the various intersections (for instance P(A∩B)=0.07 ) determine P(A) (ii) P(B∩C) (iii) P(A∩B) (iv) P(A∩B) (v) P(B∩C) (vi) probability of exactly one of the three events.
View SolutionThe accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance,P(A∪B)=0.7]. Determine
(i) P (A)
(ii) P(B∩−C)
(iii) P(A∪B)
(iv) P(A∩−B)
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.
View Solution
Knowledge Check
Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.
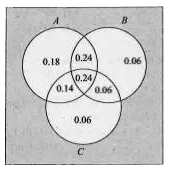
Which of the following is not true ?AA and B are independentBB and C are independentCA and C are independentDA and B∩C are independent
The accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance,P(A∪B)=0.7]. Determine
(i) P (A)
(ii) P(B∩−C)
(iii) P(A∪B)
(iv) P(A∩−B)
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.
View SolutionThe following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.

View SolutionThe following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.

View SolutionA and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.535.
(i) P(A∪B) (ii) P(A'∩B')
(iii) P(A∩B') (iv) P(B∩A')
View SolutionA and B are two events such that
P(A)=0.54,P(B)=0.69 and P(A∩B)=0.35
Find (i) P(A∪B) (ii) P(A'∩B')
(iii) P(A∩B') (iv)P(B∩A')
View SolutionA and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.35.
(i) P(A∪B) (ii) P(A'∩B')
(iii) P(A∩B') (iv) P(B∩A')
View SolutionA and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.35.
Find (i) P(A∪B) (ii) P(A'∩B') (iii) P(A'∩B)
(iv) P(B∩A')
View Solution
