Fill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are...
To solve the given question, we will fill in the blanks based on the properties of parallel lines and transversals.
1. Understanding the Properties:
- When two parallel lines are intersected by a transversal, certain angle relationships are established. We need to recall these properties to fill in the blanks.
2. First Statement:
- The first statement is: "If two parallel lines are intersected by a transversal, then each pair of corresponding angles are..."
- According to the properties of parallel lines, corresponding angles are equal. Therefore, we fill in the blank with "equal".
- Answer: If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
3. Second Statement:
- The second statement is: "If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are..."
- The interior angles on the same side of the transversal are supplementary, which means their sum is 180 degrees. Therefore, we fill in the blank with "supplementary".
- Answer: If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
Final Answers:
(i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
---
- When two parallel lines are intersected by a transversal, certain angle relationships are established. We need to recall these properties to fill in the blanks.
- The first statement is: "If two parallel lines are intersected by a transversal, then each pair of corresponding angles are..."
- According to the properties of parallel lines, corresponding angles are equal. Therefore, we fill in the blank with "equal".
- Answer: If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
- The second statement is: "If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are..."
- The interior angles on the same side of the transversal are supplementary, which means their sum is 180 degrees. Therefore, we fill in the blank with "supplementary".
- Answer: If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
(i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
Topper's Solved these Questions
Similar Questions
Which of the following statements are true (T) and which are false (F)? Give reasons.
(i)If two lines are intersected by a transversal, then corresponding angles are equal.
(ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(iii)Two lines perpendicular to the same line are perpendicular to each other.
(iv)Two lines parallel to the same line are parallel to each other.
(v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.View SolutionTheorem 6.4 : If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
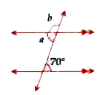 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
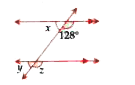 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
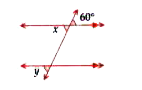 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
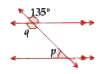 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
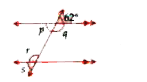 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
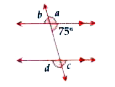 View Solution
View Solution

