Two straight lines AB and CD intersect one another at the point O. If ∠AOC+∠COB+∠BOD=2740, then ∠AOD=
86∘
90∘
94∘
127∘
The correct Answer is:A
To solve the problem, we need to find the angle ∠AOD given that the sum of the angles ∠AOC+∠COB+∠BOD=274∘.
1. Understanding the Angles:
- When two straight lines intersect, they form four angles around the point of intersection. In this case, the angles are ∠AOB,∠BOC,∠COD, and ∠DOA.
2. Sum of Angles Around a Point:
- The sum of all angles around point O is 360∘. Therefore, we can write:
∠AOC+∠COB+∠BOD+∠AOD=360∘
3. Substituting the Given Information:
- We know from the problem that:
∠AOC+∠COB+∠BOD=274∘
- We can substitute this into the equation from step 2:
274∘+∠AOD=360∘
4. Solving for ∠AOD:
- To find ∠AOD, we rearrange the equation:
∠AOD=360∘−274∘
- Now, perform the subtraction:
∠AOD=86∘
5. Conclusion:
- Therefore, the measure of angle ∠AOD is 86∘.
Final Answer:
∠AOD=86∘
- When two straight lines intersect, they form four angles around the point of intersection. In this case, the angles are ∠AOB,∠BOC,∠COD, and ∠DOA.
- The sum of all angles around point O is 360∘. Therefore, we can write:
∠AOC+∠COB+∠BOD+∠AOD=360∘
- We know from the problem that:
∠AOC+∠COB+∠BOD=274∘
- We can substitute this into the equation from step 2:
274∘+∠AOD=360∘
- To find ∠AOD, we rearrange the equation:
∠AOD=360∘−274∘
- Now, perform the subtraction:
∠AOD=86∘
- Therefore, the measure of angle ∠AOD is 86∘.
∠AOD=86∘
Topper's Solved these Questions
Similar Questions
Two lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=2700 , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
View SolutionTwo lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=2700 , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
View SolutionIn Figure, lines AB and CD intersect at O. If ∠AOC+ ∠BOE=700and ∠BOD=400, find ∠BOE and reflex ∠COE
View SolutionTwo straight lines AB and CD cut each other at O. If ∠BOD=630 , then ∠BOC= (a) 630 (b) 1170 (c) 170 (d) 1530
View SolutionABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
View SolutionIn Figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF .
View SolutionIn a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionLine segments AB and CD intersect at O such that AC=DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= (a)1000 (b) 800 (c) 900 (d) 1350
View SolutionIn Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
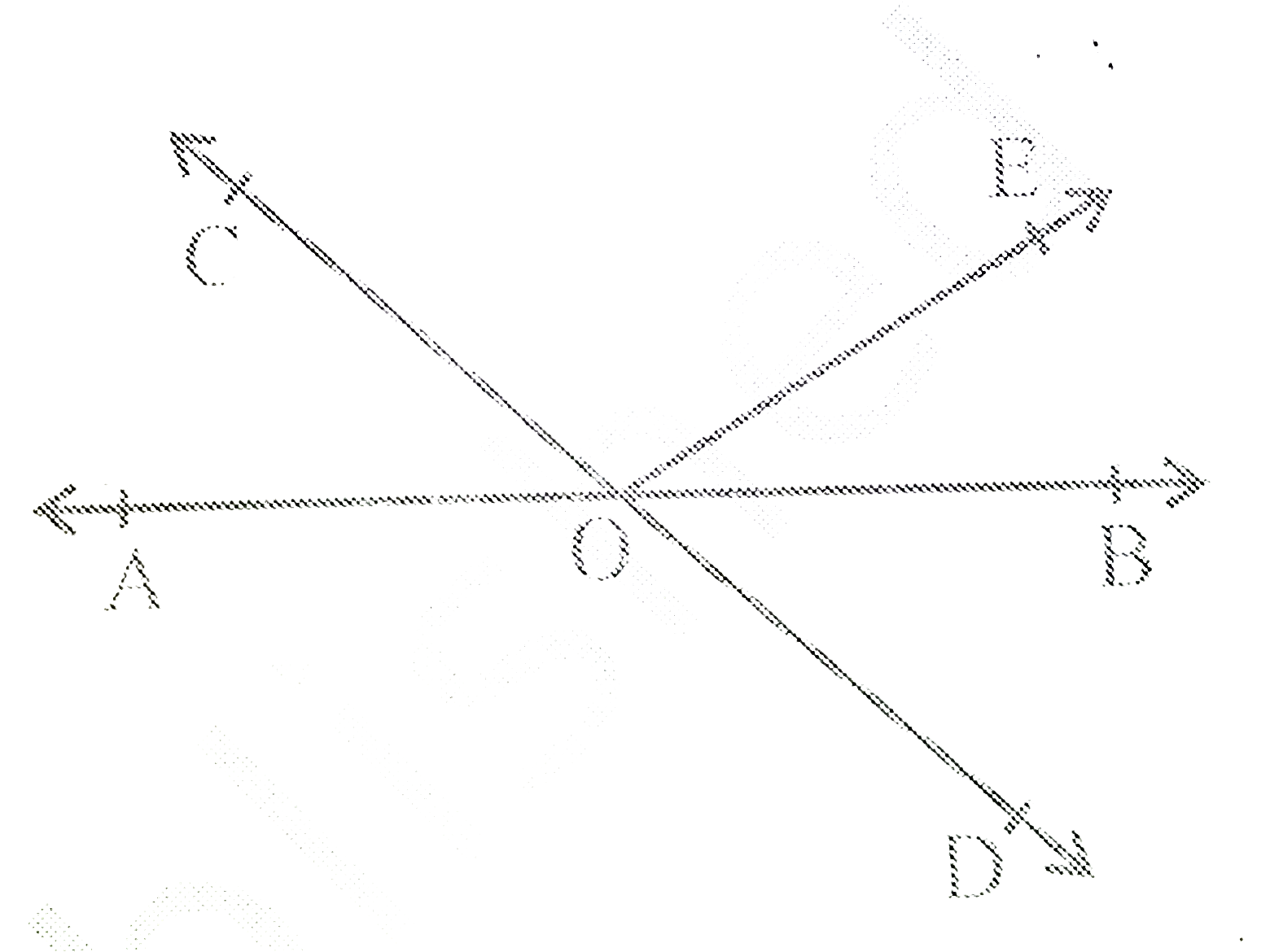
View Solution
