Find k so that x2+2x+k is a factor of 2x4+x3−14x2+5x6. Also find all zeroes of two polynomials.
The correct Answer is:N/a
Let p(x)=2x4+x3−14x2+5x+6
and g(x)=x2+2x+k
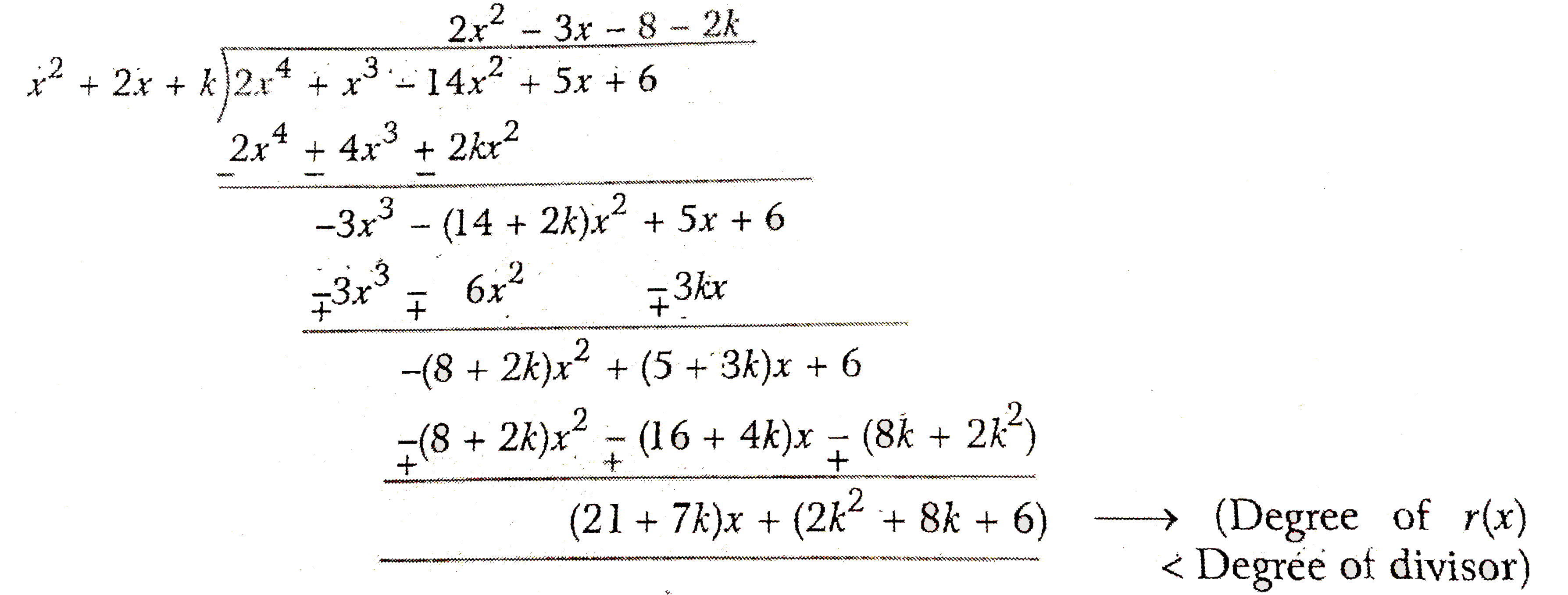
But remainder =0
⇒ (21+7k)x+(2k2+8k+6)=0
⇒ 21+7k=0 and 2k2+8k+=0
⇒ 7k=−21 and k2+4k+3=0
⇒ k=−3 and (k+3)(k+1)=0
⇒ k=−3 and k=−3ork=−1
∴ k=−3
Now, q(x)=2x2−3x−8−2k=2x2−3x−8+6=2x2−3x−2
=2x2−4x+x−2=2x(x−2)+1(x−2)=(x−2)(2x+1)
Its zeroes are given by x-2=0 and 2x+1=0
⇒ x=2andx=−12
and g(x)=x2+2x+k=x2+2x−3=x2+3x−x−3
=x(x+3)−1(x+3)=(x+3)(x−1)
Its zeroes are given by x+3=0 and x-1=0
⇒ x=-3 and x=1
∴ Zeroes of g(x) are-3and 1 and zeroes of p(x) are -3, 1, 2 and −12 Ans.
Topper's Solved these Questions
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Exercise 2a
28 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Exercise 2b
20 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions
4 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions
8 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise Very Short Answer/short Answer Questions
16 Videos
Similar Questions
Find k so that x2+2x+k is a factor of 2x4+x3−14x2+5x+6. Also find all zeroes of two polynomials.
View SolutionFind K, so that x2+2x+K is a factor of 2x4+x3−14x2+5x+6 . Also find all the zeros of the two polynomials.
View SolutionFind k so that x2−3x+k is a factor of polynomial x3−6x2+11x−6. Also find all the zeroes of the two polynomial.
View SolutionThe value of k, if x2+2x+k is a factor of 2x4+x3−14x2+5x+6 is
View SolutionThe value of k, if x2+2x+k is a factor of 2x4+x3−14x2+5x+6 is
View SolutionIf x+2k is a factor of p(x)=x5−4k2x3+2x+2k+3 . Find k.
View SolutionIf x+2k is a factor of x5−4k2x3+2x+2k+3 then find k
View SolutionIf 1 and -1 are zeroes of the polynomial x3+5x2−x−5, then find all zeroes of the given polynomial.
View SolutionIf 1 and -1 are zeroes of the polynomial x3+5x2−x−5, then find all zeroes of the given polynomial.
View SolutionFind the value of 'k' if x+3, is a factor of the polynomial x4−x3−11x2−x+k.
View Solution
