Find tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)
Video Solution
Text Solution
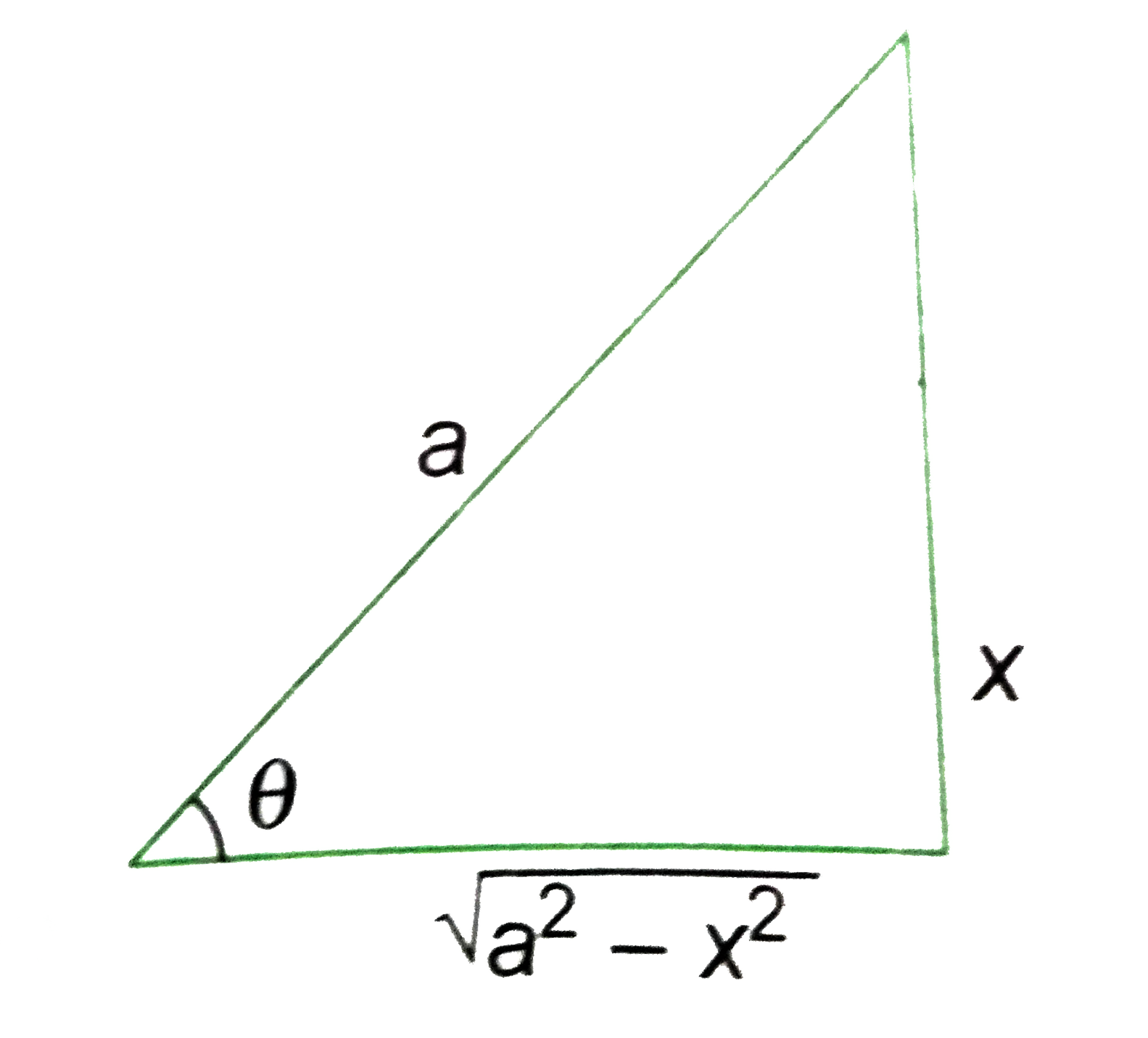
We have tan−1(x)√a2−x2=θ
From the triangle,
tan−1(x)√a2−x2=sin−1(x)a
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.26videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Knowledge Check
- Question 1 - Select One
Evaluate x√a2+x2 where a=xtanθ.
Asec2θBcosθC0Dtanθ - Question 2 - Select One
If y=tan−1x1+√(1−x2)+sin{2tan−1√(1−x1+x)} then dy/dx=
Ax√(1−x2)B1−2x√(1−x2)C1−2x2√(1−x2)D1(1−x2)
tan−1x√1−x2withrespecttosin−1(2x√1−x2)
View SolutionDifferentiate tan−1(x√1−x2) with respect to sin−1(2x√1−x2), if −1√2<x<1√2
View SolutionProve that sin−1.((x+√1−x2√2)=sin−1x+π4, where −1√2<x<1√2
View SolutionProve that
tan−1(1−√x1+√x)=π4−tan−1√x,wherex>0View SolutionProve that tan−1{xa+√a2−x2}=12sin−1xa,−a<x<a
View SolutionProve that sincot−1tancos−1x=sincosec−1cottan−1x=x, where x∈[0,1]
View Solution

