Find the area bounded by curves ${(x - 1)}^{2} + y^{2} = 1$ and $x^{2} + y^{2} = 1$ .

Video Solution

Text Solution

Verified by Experts

Curve ${(x - 1)}^{2} + y^{2} = 1$ …(1)
$∴ y = \sqrt{1 - {(x - 1)}^{2}}$
Represents a circle whose centre is (1, 0) and radius is 1.

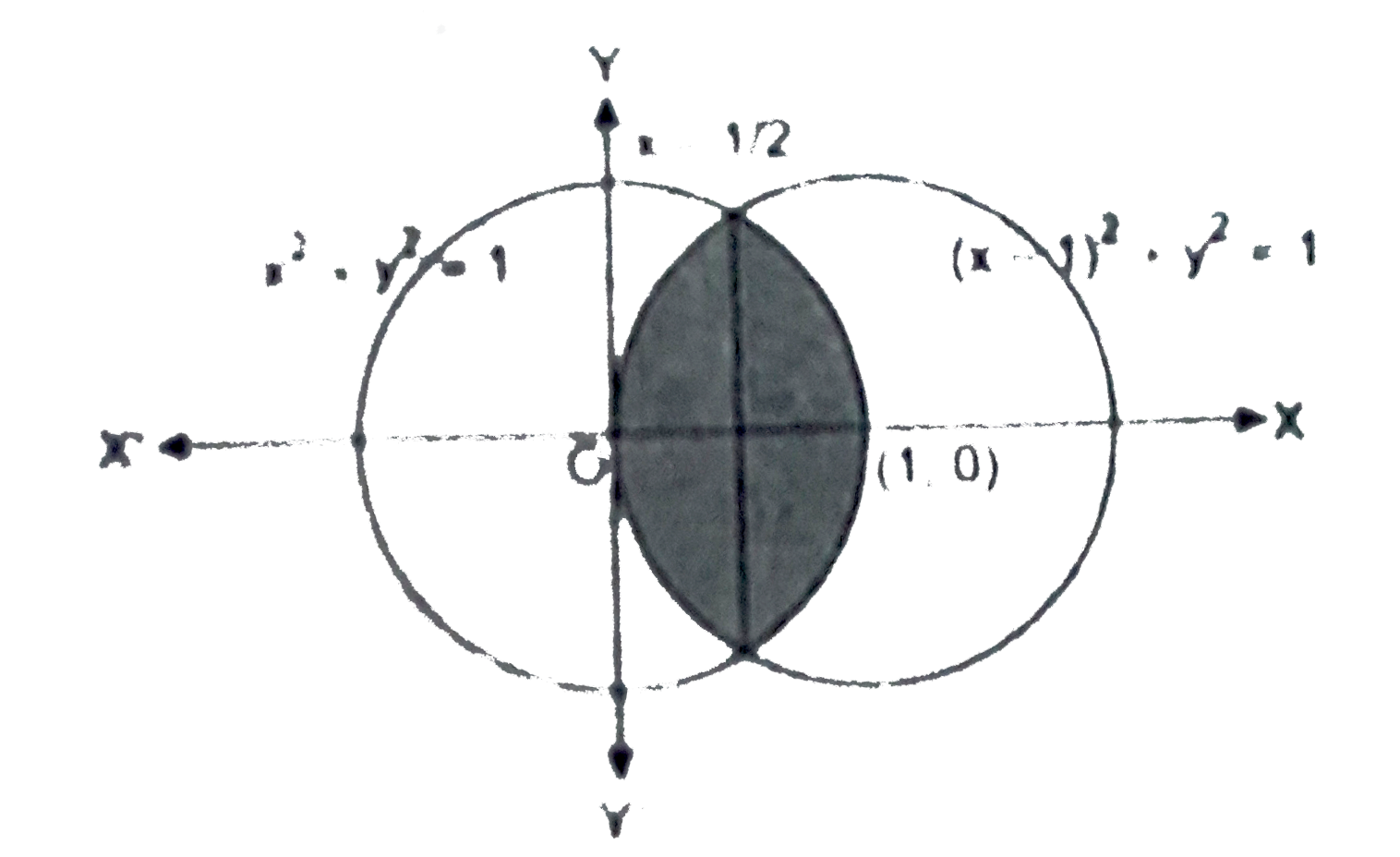
and curve, $x^{2} + y^{2} = 1$ ...(2)
$∴ y = \sqrt{1 - x^{2}}$
Represents a circle whose centre is (0, 0) and radius is 1.
Two circles meet at ${(x - 1)}^{2} = x^{2}$
$\Rightarrow 2 x = 1 \Rightarrow x = \frac{1}{2}$
$∴$ Required area (shaded region)
$= 2 [\int_{0}^{1 / 2} y_{1} d x + \int_{1 / 2}^{1} y_{2} d x]$
$= 2 [\int_{0}^{1 / 2} \sqrt{1 - {(x - 1)}^{2}} d x + \int_{1 / 2}^{1} \sqrt{1 - x^{2}} d x]$
$= 2 {[\frac{x - 1}{2} \sqrt{1 - {(x - 1)}^{2}} + \frac{1}{2} {sin}^{- 1} \frac{x - 1}{1}]}_{0}^{- 1} + 2 {[\frac{x}{2} \sqrt{1 - x^{2}} + \frac{1}{2} {sin}^{- 1} x]}_{1 / 2}^{- 1}$
$= 2 ⎡ ⎣ \frac{\frac{1}{2} - 1}{2} \sqrt{1 - \frac{1}{4}} + \frac{1}{2} {sin}^{- 1} (- \frac{1}{2}) - (\frac{- 1}{2}) 0 - \frac{1}{2} {sin}^{- 1} (- 1) ⎤ ⎦ + 2 [0 + \frac{1}{2} {sin}^{- 1} (1) - \frac{1}{4} \sqrt{1 - \frac{1}{4}} - \frac{1}{2} {sin}^{- 1} \frac{1}{2}]$
$= 2 [- \frac{1}{4} \cdot \frac{\sqrt{3}}{2} - \frac{1}{2} \cdot \frac{π}{6} + 0 + \frac{1}{2} \cdot \frac{π}{2}] + \frac{π}{2} - \frac{1}{2} \cdot \frac{\sqrt{3}}{2} - \frac{π}{6}$
$= - \frac{\sqrt{3}}{4} - \frac{π}{6} + \frac{π}{2} + \frac{π}{2} - \frac{\sqrt{3}}{4} - \frac{π}{6}$
$= (\frac{2 π}{3} - \frac{\sqrt{3}}{2})$ sq. units.

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Exercise 8.2

Home
Ask Doubt
Profile