Find the area bounded by the curve f(x)=x+sinxand its inverse function between the ordinates x=0 to x=2π.
Video Solution
Text Solution
y=x+sinx
∴ dydx=1+osx≥0∀x
Also d2ydx2=−sinx=0 when x=nπ,n∈Z
Hence x=nπ are points of inflection, where curve changes its concavity.
Also, for x∈(0,π),sinx>0⇒x+sinx>x
And for x∈(π,2π),sinx<0⇒x+sinx<x
Thus, we have following graphs of function y=f(x) and its inverse function.
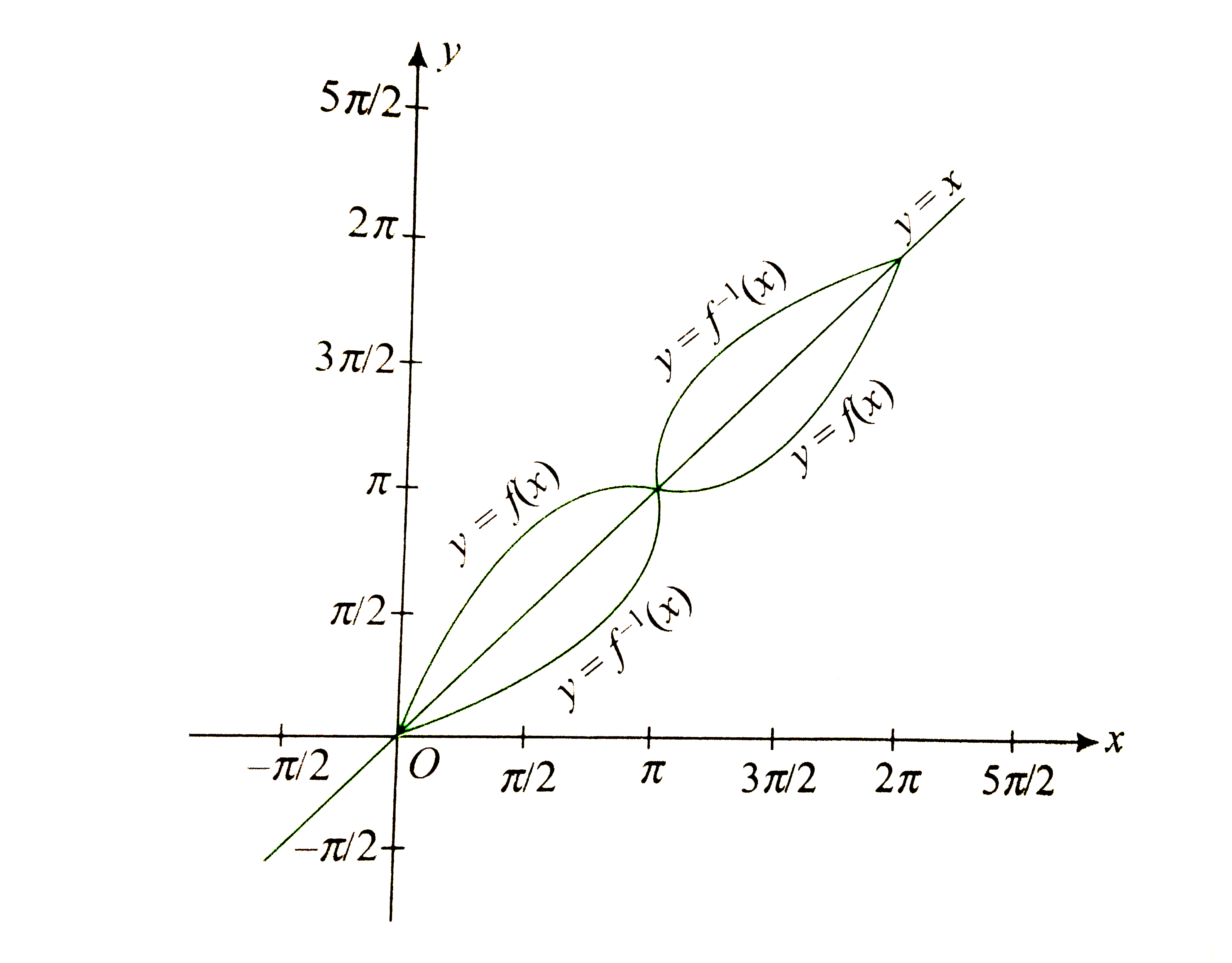
Required area =4∫π0(f(x)−x)dx
=4∫π0sinxdx=4×2=8 sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Find the area bounded by the curve y =sin x between x=0 and x=2π.
A1 sq unitB2 sq unitsC3 sq unitsD4 sq unitsChoose the most appropriate options.
The area bounded by the curves y =cos x and y = sin x between the ordinates x=0 and x=3π2 isA4√2−1B4√2+1C4√2−2D4√2+2
Find the area bounded by the curve y=cosxbetween x=0and x=2π.
View SolutionFind the area bounded by the curve y=cosx between x=0andx=2π
View SolutionFind the area bounded by the curve y=sinx between x=0 and x=2π.
View SolutionFind the area bounded by the curve f(x) = maximum {1+sinx,1,1−cosx} and the x-axis between the ordinates x=−πandx=π.
View SolutionFind the area bounded by the curve y=x sins-axis in the interval 0≤x≤2π.
View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3) and x-axis lying between the ordinates x=0andx=4 is
View Solution
