Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
Video Solution
Text Solution
The given curves are
x2=y (1)
x2=−y (2)
y2=4x−3 (3)
Clearly (1) and (2) meet at (0,0).
Solving (1) and (3), we get x4−4x+3=0
or (x−1)(x3+x2+x−3)=0
or (x−1)2(x2+2x+3)=0
⇒ x=1⇒y=1
Thus, point of intersection is (1,1)
Similarly, point of intersection of (2) and (3) is (1,-1).
The graphs of three curves are as shown in the figure.
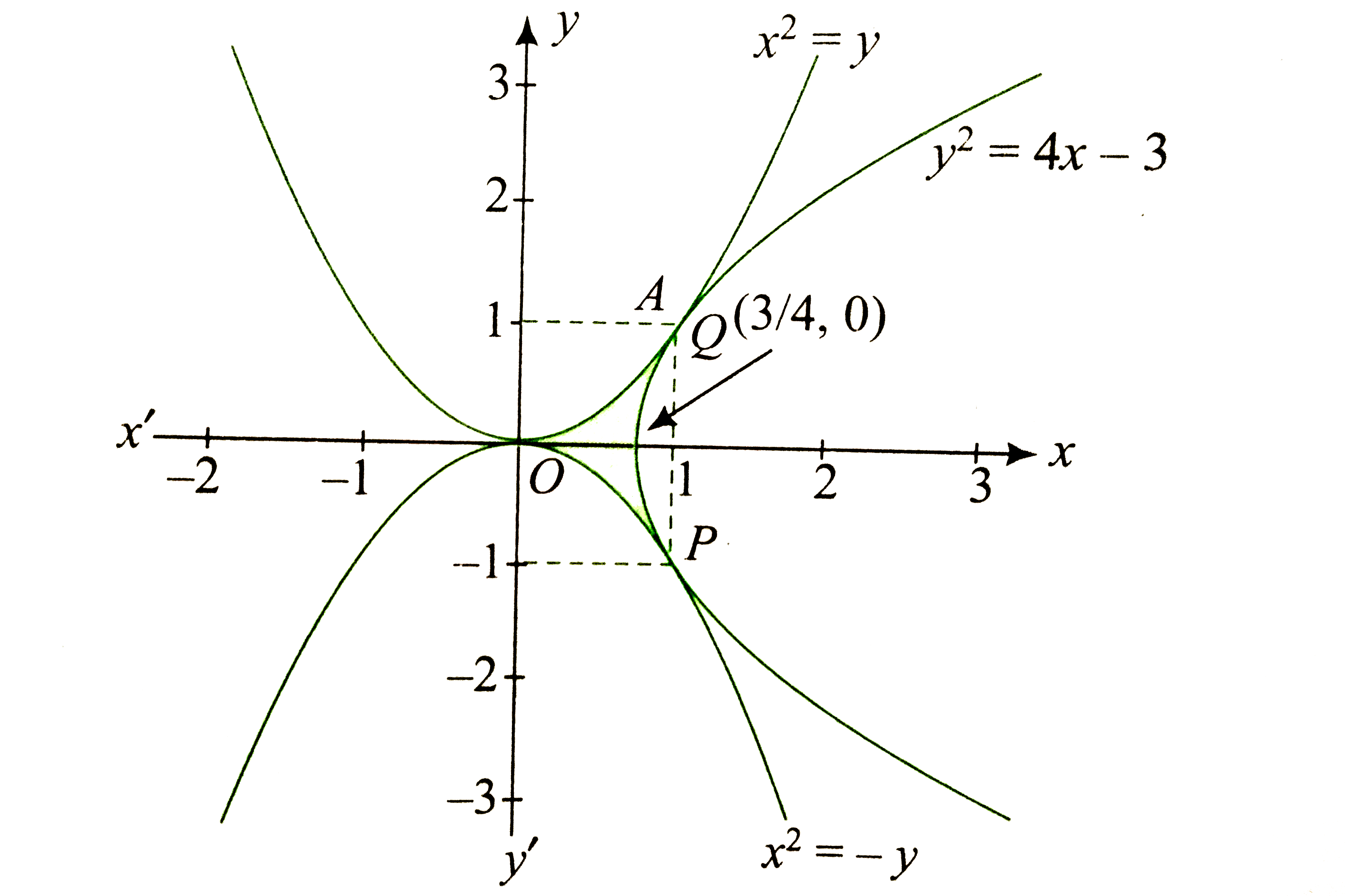
We also observe that at x=1andyy=1,dydx for (1)and(3) is same
and hence the two curves touch each other at (1,1).
Same is the case with (2) and (3) at (1,-1).
Required area = Shaded region in the figure
=2(Ar OPQA)
2[∫10x2dx−∫13/4√4x−3dx]
=2⎡⎢⎣(x23)10−(2(4x−3)3/24×3)13/4⎤⎥⎦=2[13−16]
=13 sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Find area bounded by the curves x2≤y≤x+2
A112B72C92D52
Find the area bounded by the curves y=x3−xandy=x2+x.
View SolutionFind the area bounded by the curve 4y2=9xand3x2=16y
View SolutionFind the area bounded by the curve y=4x2,x=0,x=1 and y=4 in first quadrant.
View SolutionFind the area bounded by the curve x2=4yand the line x=4y−2.
View SolutionFind the area bounded by the curves x2+y2=4 and x2+y2=4x
View SolutionFind the area bounded by the curves x2+y2=4,x2=−√2y and x = y.
View SolutionFind the area bounded by the curve y=x2+2x−3 and the line y=x+3.
View Solution
