Find the area bounded by the parabola $y = x^{2} + 1$ and the straight line $x + y = 3 .$

Video Solution

Text Solution

Verified by Experts

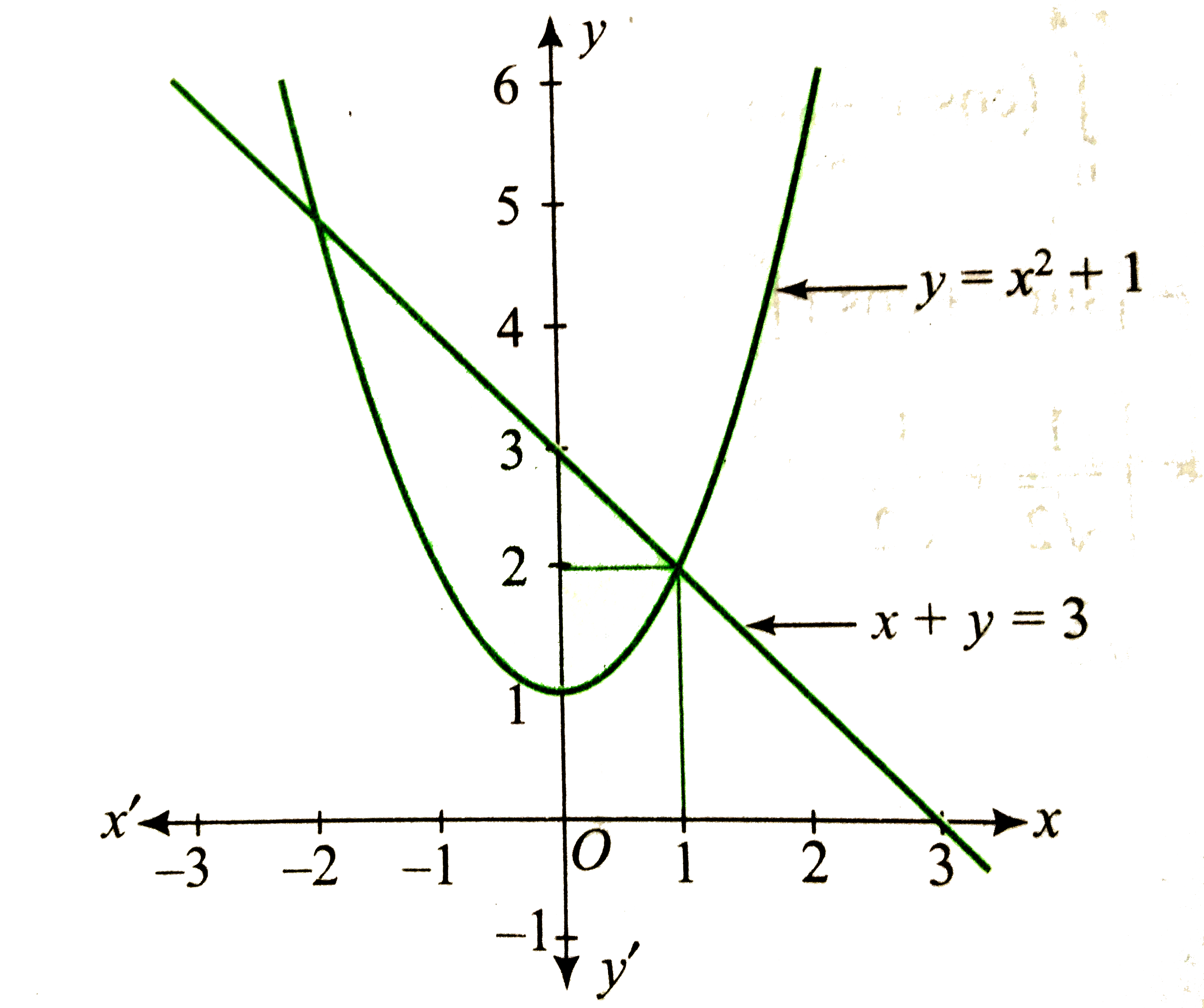
The two curves meet at points where $3 - x = x^{2} + 1$ ,
$i . e ., x^{2} + x - 2 = 0$
$or (x + 2) (x - 1) = 0 or x = - 2, 1$
$∴ Required area = \int_{- 2}^{1} [(3 - x) - (x^{2} + 1)] d x$
$= \int_{- 2}^{1} (2 - x - x^{2}) d x$
$= {[2 x - \frac{x^{2}}{2} - \frac{x^{3}}{3}]}_{- 2}^{1}$
$= (2 - \frac{1}{2} - \frac{1}{3}) - (- 4 - \frac{4}{2} + \frac{8}{3})$
$= \frac{9}{2}$ sq. units

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the area enclosed by the parabola $y = 2 - x^{2}$ and the straight line x + y = 0
A $\frac{17}{6}$
B $\frac{34}{7}$
C $\frac{9}{2}$
D $\frac{7}{2}$
The area of the region bounded by the parabola $y = x^{2} - 4 x + 5$ and the straight line $y = x + 1$ is
A $1 / 2$
B2
C3
D $9 / 2$

CENGAGE-AREA-Comprehension Type

Home
Ask Doubt
Profile