Find the area bounded by y=−x3+x2+16xandy=4xSolution in Bengali
Solving given curve, we have
−x3+x2+16x=4x
∴ x=0orx2−x−12=0
⇒ x=0or(x−4)(x+3)=0
⇒ x=0orx=−3,4
Now y=−x3+x2+16
=−x(x2−x−16)
If y=0 then x=0orx2−x−16=0
∴ x=0orx1±√652
From the above in information we having following graphs.
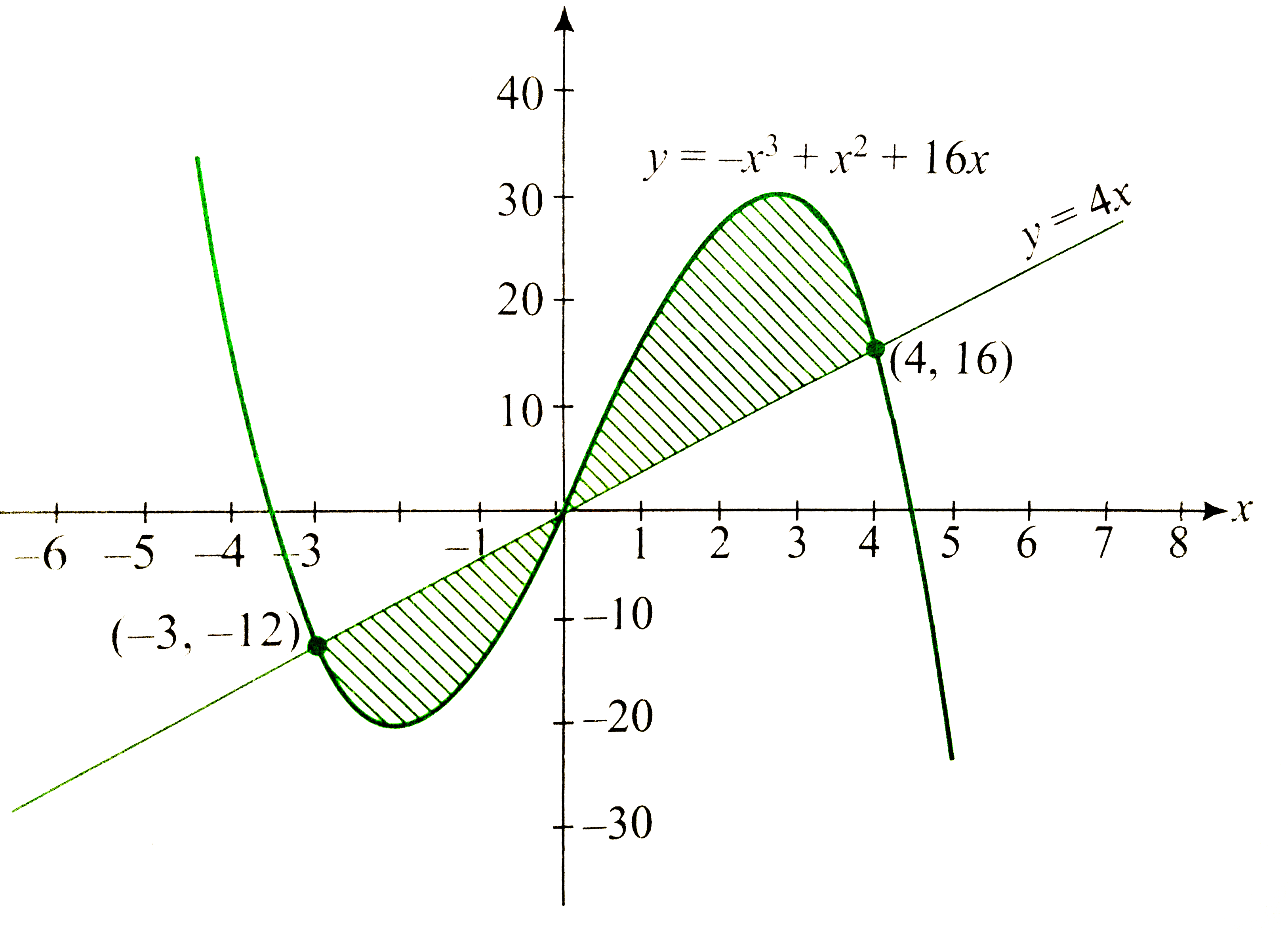
From the figure area of the shaded region,
A=0∫−3[4x−(−x3+x2+16x)]dx+4∫0[(−x3+x2+16x)−4x]dx
=0∫−3(x3−x2−12x)dx+4∫0(−x2+x2+12x)dx
=[x44−x33−6x2]0−3+[−x44+x33+6x2]40
=[−814−9+54]+[−64+643+96]
=93712 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples10videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
02:37View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
06:15View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
06:51View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:15View SolutionThe area bounded by the x-axis and the curve y=4x−x2−3 is
03:13View SolutionFind the area bounded by y=−x3+x2+16xandy=4x
07:33View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
04:13View SolutionFind the area of the region bounded by the parabolas y2=4xandx2=4y
04:09View SolutionThe area bounded by the X-axis and the curve y=4x−x2−3 is
01:56View SolutionFind the area bounded by the curves x2=y, x2=−y and y2=4x−3
04:47View SolutionFind the area bounded by y=−x3+x2+16xandy=4x
02:53View SolutionFind the area bounded by the parabolas : y2=16x and x2=16y.
05:03View SolutionFind the area of the region bounded by
y=x2andy=x307:06View Solutionfind the area of the region bounded by 'y^2=4x' and x=2
03:06View SolutionThe area bounded by x-axis and the curve y=4x−x2−3 is
04:51View Solution

