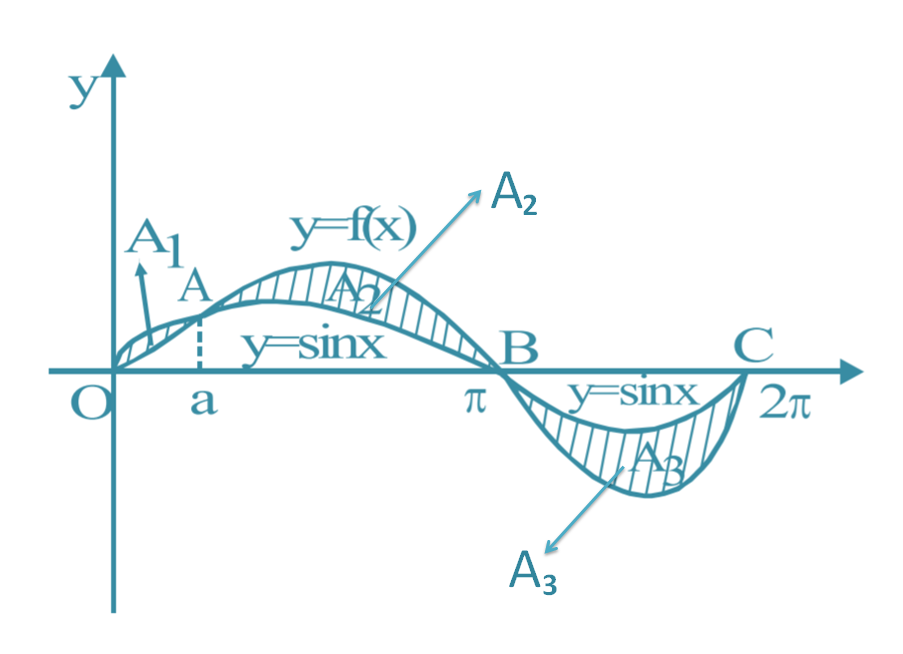
In the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, is the area bounded by the curves as shown in the figure, respectively, for .
If a, then

The function f(x) isSolution in Bengali
The correct Answer is:B
Differentiating w.r.t. 'a' both sides.
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
If the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionA function y=f(x) satisfies the condition f'(x)sin x+f(x)cos x=1,f(x) being bounded when x rarr0. If I=int_(0)^((pi)/(2))f(x)dx then (A)(pi)/(2)
View SolutionA function y=f(x) satisfies f(x)=-(1)/(x^(2))-pi^(2)sin(pi x);f'(2)=pi+(1)/(2) and f(1)=0. The value of f((1)/(2))
View SolutionA function y=f(x) satisfies f''(x)=−1x2−π2sin(πx), f'(2)=π+12 and f(1)=0then value of f(12) is
View SolutionWhich of the following functions is/are discontinuous at x=0?f(x)=sin((pi)/(2x)),x!=0 and f(x)=1
View Solutionf(x)={1;x<0 and 1+sin x;f or 0<=x<=(pi)/(2), then check the differentiability of the function f(x) at x=0.
View SolutionConsider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axis
View SolutionArea bounded by y=f−1(x) and tangent and normal drawn to it at points with abscissae π and 2π, where f(x)=sinx−x is
View SolutionIn the adjacent figure the graph of two function y=f(x) and y=sinx are given y=sin x intersects, y=f(x) at A(a,f(a)),B(π,0)andC(2π,0).
Ai(i=1,2,3) is the area bounded by the curves y=f(x)andy=sinx between x=0 and x=a,i=1 between x=a and x=π,i=2 between x=π and x=2π,i=3. If A1=1−sina+(a−1) cos a, determine the function f(x). Hence, determine a and A1. Also, calculate A2andA3.
 .
.
View SolutionLet f (x) be a continous function such that the area bounded by the curve y=f(x) x-axis and the lines x=0 and x=aisa22+a2sina+π2cosa, then f(π2) is
View SolutionConsider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axis
View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then

The function f(x) is
View Solutionएक फलन y=f(x),f''(x)=−1x2−π2sin(πx),f'(2)=π+12 को संतुष्ट करता है तथा f(1)=0 है तो f(12) का मान है।
View Solutionदिए गये चित्र में दो फलन y=f(x) तथा y=sinx एक दुसरे को बिन्दु A(a,f(a)),B(π,0) तथा C(2π,0) पर काटते है | Ai(i=1,2,3) वक्र y=f(x) तथा y=sinx का x=0 तथा x=a के मध्य क्षेत्रफल, (i=1),x=a तथा x=π के मध्य, (i=2),x=π तथा x=2π के मध्य, (i=3) है| यदि Ai=1−sina+(a−1)cosa तो फलन f(x) ज्ञात कीजिए 'a',A1,A2 तथा A3 के मान ज्ञात कीजिए |
View Solution