Find the area of ΔABC with A(1,−4) and midpoints of sides through A being (2,−1) and (0,−1).
19 sq units
14 sq units
13 sq units
12 sq units
The correct Answer is:D
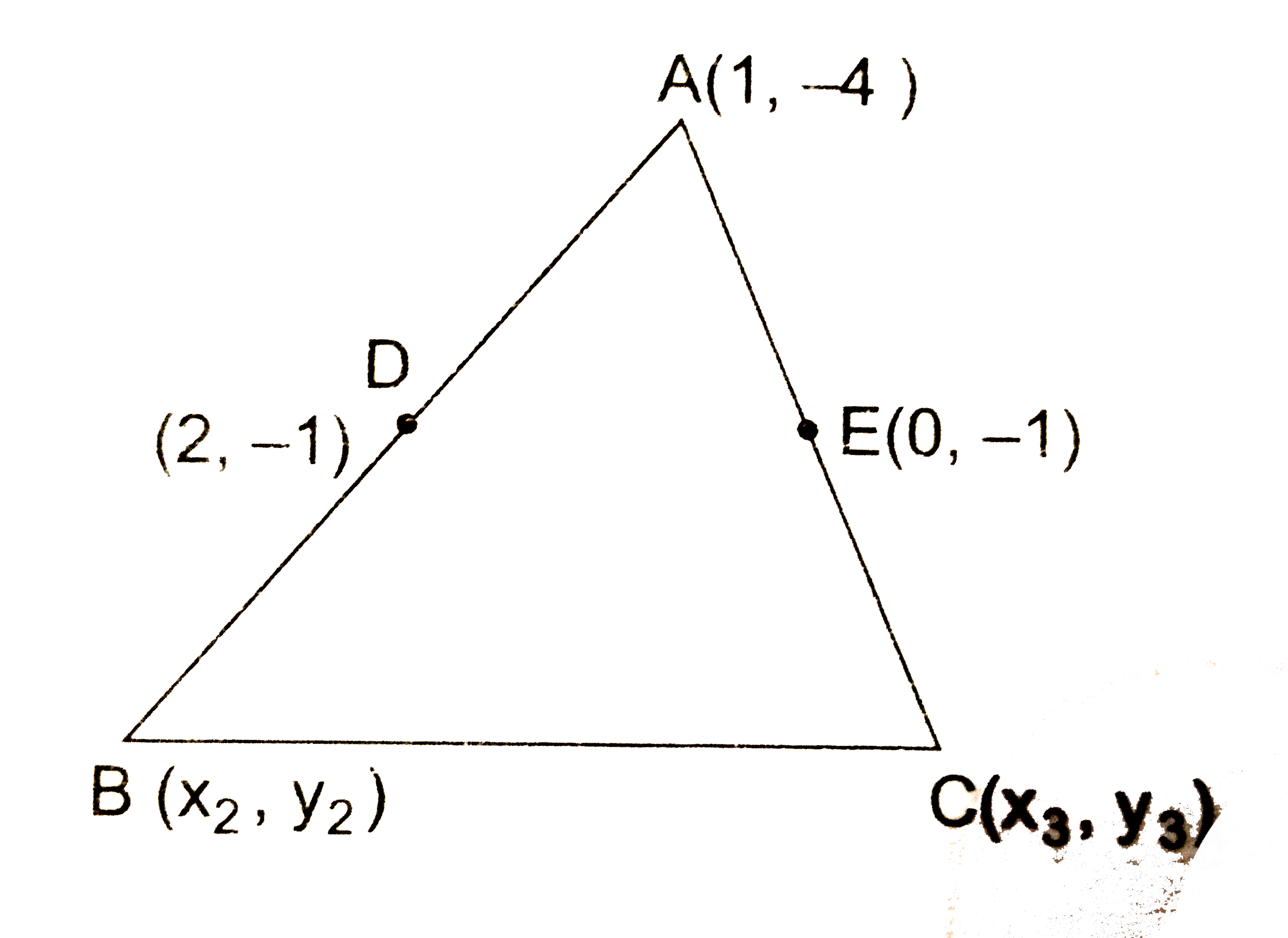
Let the vertices of ΔABC be A(1, -4), B(x2,y2)and C(x3,y3).
Let D(2, -1) and E(0, -1) be the midpoints of AB and AC respectively. Then,
1+x22=2,−4+y22=−1
⇒1+x2=4,k−4+y2=−2.
⇒x2=3,y2=2.
And,1+x32=0,−4+y32=−1
⇒1+x3=0,−4+y3=−2
⇒x3=−1,y3=2.
In ΔABC, we have
A(x1=1,y1=−4),B(x2=3,y2)andC(x3=−1,y3=2)
Now, find ar(ΔABC).
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 6D
17 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 6B
38 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
Similar Questions
Find the area of the triangle ABC with A(1,−4) and mid-points of sides through A being (2,−1)and(0,−1).
View SolutionFind the area of the triangle PQR with Q(3, 2) and the mid-points of the sides through Q being (2, −1) and (1, 2) .
View SolutionFind the area of △ABC, the midpoints of whose sides AB, BC and CA are D(3,-1), E(5, 3) and F(1,-3) respectively.
View SolutionA triangle has vertex at (1,2) and the midpoints of the two sides through it are (-1,1) and (2,3). Then the centroid of this triangle is
(13,1)
(13,2)
(1,73)
(13,53)
View SolutionFind the area of a triangle ABC if the coordinates of the middle points of the sides of the triangle are (−1,−2),(6,1)and(3,5)
View SolutionIf the vertex of a triangle is (1 , 1) and the midpoints of two sides of the triangle through this vertex are (-1 , 2 ) and (3 , 2) , then the centroid of the triangle is :
View SolutionFind the area of the triangle formed by the mid points of sides of the triangle whose vertices are (2,1),1−2,3),(4,−3)
View SolutionFind the area of the triangle ΔABC in which a=1, b=2 and ∠c=600.
View SolutionFind the area of ΔABC with vertices A(0, -1), B(2, 1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides.
Show that the ratio of the areas of two triangles is 4:1.
View Solution21. If a vertex of a triangle is (1, 1) and the midpoints of two sides of the triangle through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is
View Solution
