Find the area of the circle 4x2+4y2=9which is interior to the parabola x2=4y.
Video Solution
Text Solution
Given equation of circle is 4x2+4y2=9 and equation of parabola is x2=4y.
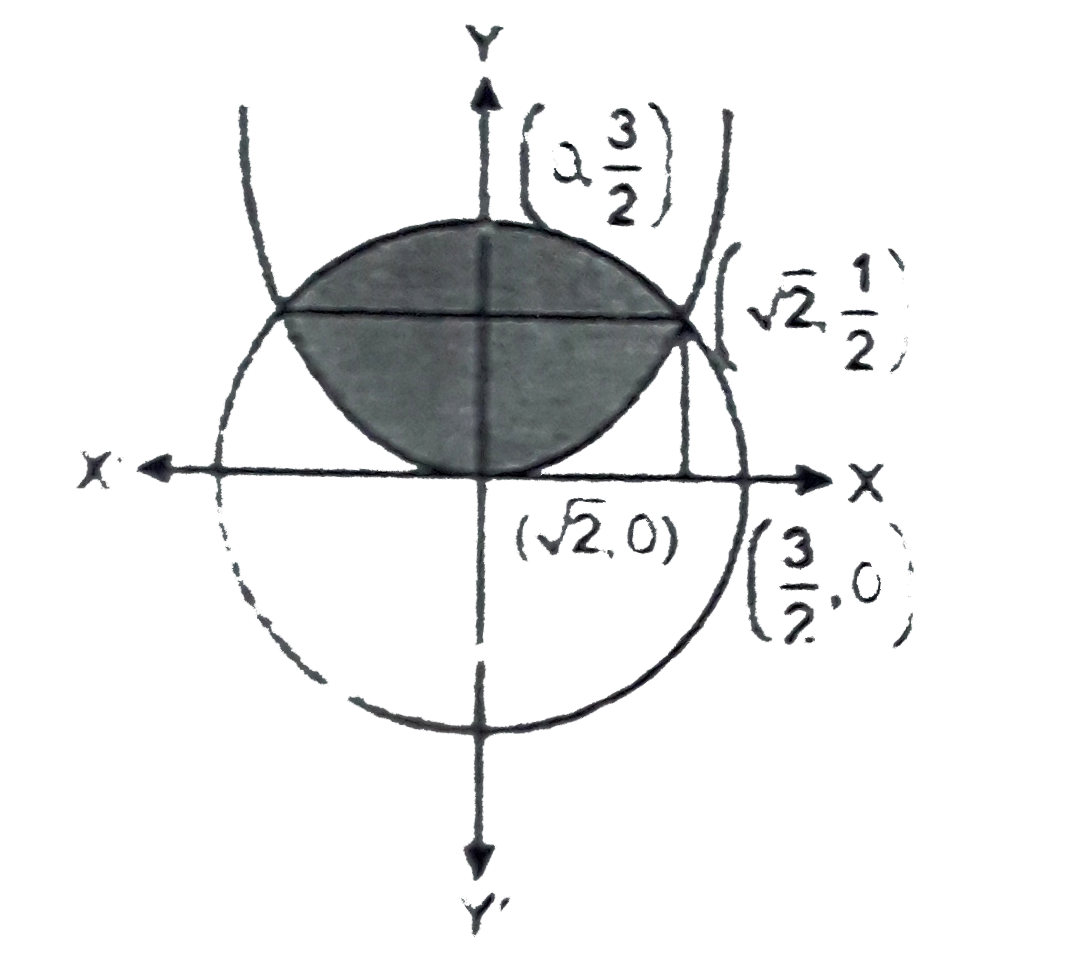
Now, solving the equations of two curves,
4(4y)+4y2=9
⇒4y2+16y−9=0
⇒y=−16±√256+1442×4
=−16±√4008
=−16±208=12,−92
but y gt 0, so two curves will meet when y=12,
∴x2=4×12=2
⇒x=±√2
∴ Required area=2∫√20(y2−y1)dx
={∫√20√9−4x24dx−∫√20x24dx}
=2∫√20√(32)2−x2dx−24[x33]√20
=2⎡⎣x2√(32)2−x2+(3/2)22sin−1(x3/2)⎤⎦√20−16[(√2)3−0]
=[x√94−x2+94sin−1(2x3)]√20−2√26
=[√2√94−2+94sin−1(2√23)]−{0−0}−2√26
=√22+94sin−1(2√23)−2√26
=(√22−√23)+94sin−1(2√23)
=√26+94sin−1(2√23) sq. units.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.1
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise
24 Videos
- Continuity and DifferentiabilityBOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Knowledge Check
The equations of the tangents of the circle x2+y2=9 which are parallel to line 3x+4y=0 are
A3x+4y+15=0B4x-3y+15=0C4x+3y+15=0D3x+4y+45=0The equation of the common tangents to the circle(x−3)2+y2=9 and the parabola y2=4x the x-axis, is
A√3y=3x+1B√3y=−(x+1)C√3y=(x+1)D√3y=−(3x+1)
Find the area of that part of the circle x2+\ y2=16 which is exterior to the parabola y2=6x.
View SolutionFind the equation of the circle which is concentric with the circle x2+y2−4x+6y−3=0 and the double of its area.
View SolutionFind the equation of line which is normal to the parabola x2=4y and touches the parabola y2=12x.
View SolutionFind the area of the region which is inside the parabola y=−x2+6x−5, out the side the parabola y=−x2+4x−3 and left of the stragiht line y=3x−15.
View SolutionFind area of the ellipse4x2+9y2=36.
View SolutionFind the area of the figure contained between the parabola x2=4y and the witch of Agnesi y=8x2+4
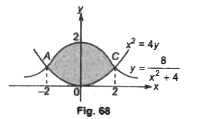
View Solution
