Find the area of the figure enclosed by the curve 5x2+6xy+2y2+7x+6y+6=0.
Video Solution
Text Solution
Equation of curve can be re-written as
2y2+6(1+x)y+5x2+7x+6=0
⇒ y1=−3(1+x)−√(3−x)(x−1)2
y2=−(1+x)+√(3−x)(x−1)2
Therefore, the curves (y1andy2) are defined for values of x for whih (3−x)(x−1)≥0, i.e., 1≤x≤3.
(Actually the given equation represents an ellipse, because Δ≠0andh2<ab.)
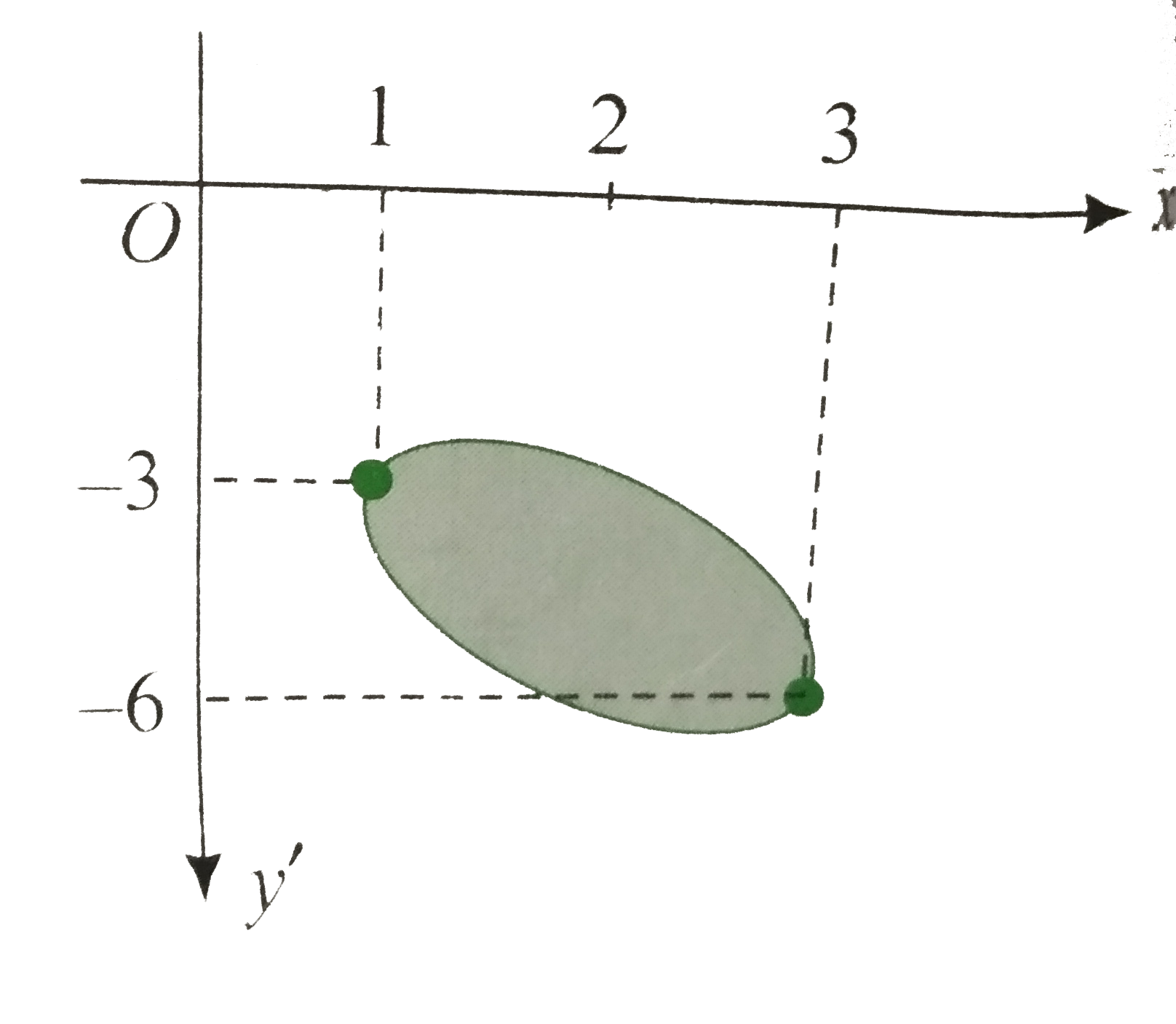
Required are will be given by
A=3∫1|y1−y2|dx⇒A=3∫1√(3−x)(x−1)dx
Put x=3cos2θ+sin2θ,i.e.,dx=−2sin2θdθ
∴ A=2π/2∫0sin22θdθ=π2 sq. units.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.214videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Find the area enclosed by the curves x^2=y , y=x+2,
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area of the region enclosed by the curves y=xlogx and y=2x−2x2.
View SolutionDraw a rough sketch of the curve y2=4x and find the area of the region enclosed by the curve and the line y=x.
View SolutionFind the area enclosed by the curve y=3x and y=6x-x2
View SolutionFind the area enclosed by the curves x2=y,y=x+2 and x-axis
View SolutionFind the area enclosed by the curves
max(2|x|,2|y|)=1View SolutionFind the area of the region enclosed by the given curves .
y=x3+3,y=0,x=−1,x=2View SolutionFind the area of the region enclosed by the given curves .
y=sinx,y=cosx,x=0,x=π2View SolutionFind the area enclosed with in the curve
y=x2,y=x3View Solution

