Find the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
To find the area of the quadrilateral ABCD, we can divide it into two triangles: triangle ABC and triangle ACD. We will calculate the area of each triangle using Heron's formula and then sum them up to get the total area of the quadrilateral.
Step 1: Calculate the area of triangle ABC
1. Identify the sides of triangle ABC:
- AB = 7 cm
- BC = 6 cm
- AC = 9 cm
2. Calculate the semi-perimeter (s) of triangle ABC:
s=AB+BC+AC2=7+6+92=222=11 cm
3. Apply Heron's formula to find the area (A) of triangle ABC:
A=√s(s−AB)(s−BC)(s−AC)
A=√11(11−7)(11−6)(11−9)=√11×4×5×2
A=√440≈20.98 cm2
Step 2: Calculate the area of triangle ACD
1. Identify the sides of triangle ACD:
- AC = 9 cm
- CD = 12 cm
- DA = 15 cm
2. Calculate the semi-perimeter (s) of triangle ACD:
s=AC+CD+DA2=9+12+152=362=18 cm
3. Apply Heron's formula to find the area (A) of triangle ACD:
A=√s(s−AC)(s−CD)(s−DA)
A=√18(18−9)(18−12)(18−15)=√18×9×6×3
A=√2916=54 cm2
Step 3: Calculate the total area of quadrilateral ABCD
1. Sum the areas of triangles ABC and ACD:
Area of quadrilateral ABCD=Area of △ABC+Area of △ACD
Area of quadrilateral ABCD=20.98+54=74.98 cm2
Final Answer:
The area of quadrilateral ABCD is approximately 74.98 cm2.
---
- AB = 7 cm
- BC = 6 cm
- AC = 9 cm
s=AB+BC+AC2=7+6+92=222=11 cm
A=√s(s−AB)(s−BC)(s−AC)
A=√11(11−7)(11−6)(11−9)=√11×4×5×2
A=√440≈20.98 cm2
- AC = 9 cm
- CD = 12 cm
- DA = 15 cm
s=AC+CD+DA2=9+12+152=362=18 cm
A=√s(s−AC)(s−CD)(s−DA)
A=√18(18−9)(18−12)(18−15)=√18×9×6×3
A=√2916=54 cm2
Area of quadrilateral ABCD=Area of △ABC+Area of △ACD
Area of quadrilateral ABCD=20.98+54=74.98 cm2
The area of quadrilateral ABCD is approximately 74.98 cm2.
Topper's Solved these Questions
Similar Questions
Calculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionWhich of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
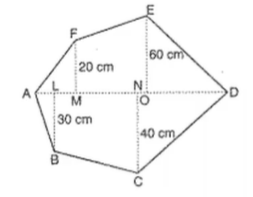
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
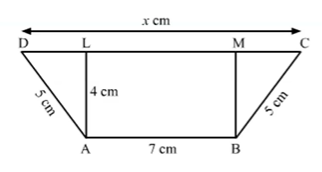
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
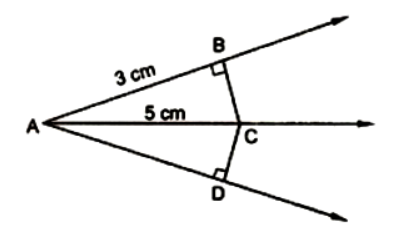
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
View SolutionIn fig. 15 ABCD is a parallelogram CM⊥AB and BL⊥AD. If AB=16 cm, AD=12 cm, CM=10 cm, find BL If AD=10cm, CM=8cm, BL=12 cm, find AB .
View Solution