Find the area of the region bounded by the curves x2+y2=4 and (x−2)2+y2=4.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

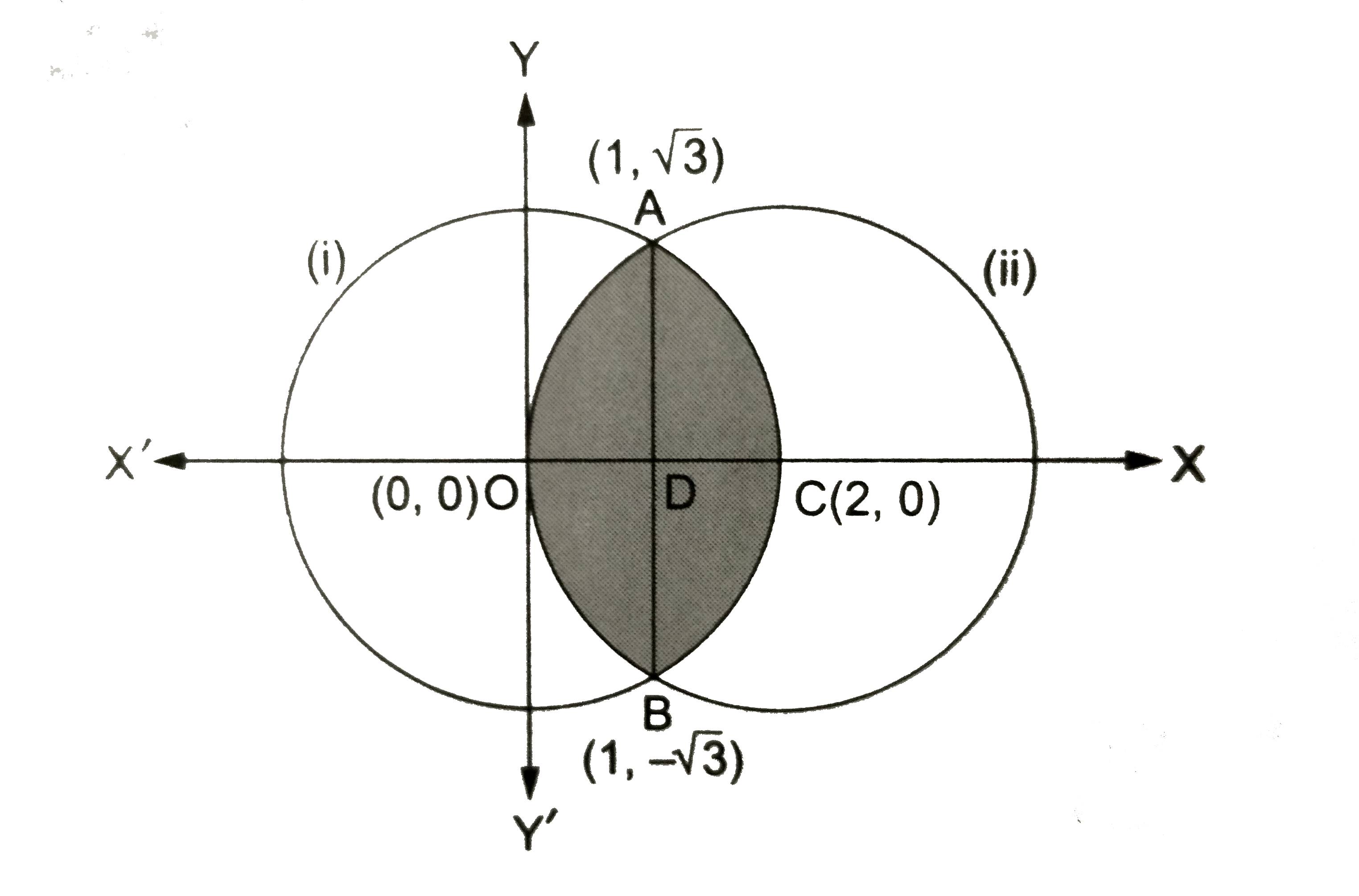
x2+y2=4 is a circle with its centre at O(0,0) and radius = 2 units And , (x−2)2=4 is a circle with is centre at C(2,0) and radius 2 units
The given circles are
x2+y2)=4 is a circle with its centre at C(2,0) and radius = 2 units.
The given cirlcles are
x2+Y2=4
and (x−2)2=4
ocr_image
Eliminating y form (i) and (ii) we get
4−x2=4−(x−2)2⇒4x=4⇒x=1
Putting x=1∈(i),we≥ty2=3⇒y=±√3
Thus the points of intersection of the two circles are A(1,3√3) and B(1,−√3)
Both the circles are symmetrical about the x-axis.
Required area =2area(AOCA)
2(area AODA + area CADC)
21∫0 y dx for circle (ii)+22∫1y dx for circle (i)
21∫0√4−(x−2)2dx+22∫1√4−x2dx
=⎡⎢ ⎢⎣(x−2)√4−(x−2)22=42sin−1x−22⎤⎥ ⎥⎦1−0+[x√4−x22+42.sin−1x2]01
=2[{(−√32+2sin−1(−12)}−{0+2sin−1(−1)}+{2sin−1(1)−√32−2sin−1(12)}]
={−√32+2(π2)−2(−π2)+(2.π2−√32−2×π6)}
=2(4π3−√3)sq units
Hence , the required area is 2(4π3−√3)sq units
ocr_image

|