Question

Find the area of the region bounded by the curves $y=x^2+2;y=x;x=0$ and $x=3$

Explanation

Given curve `y=x^(2)+2` represents a parabola whose vertex is (0, 2) and it is symmetric about Y-axis.

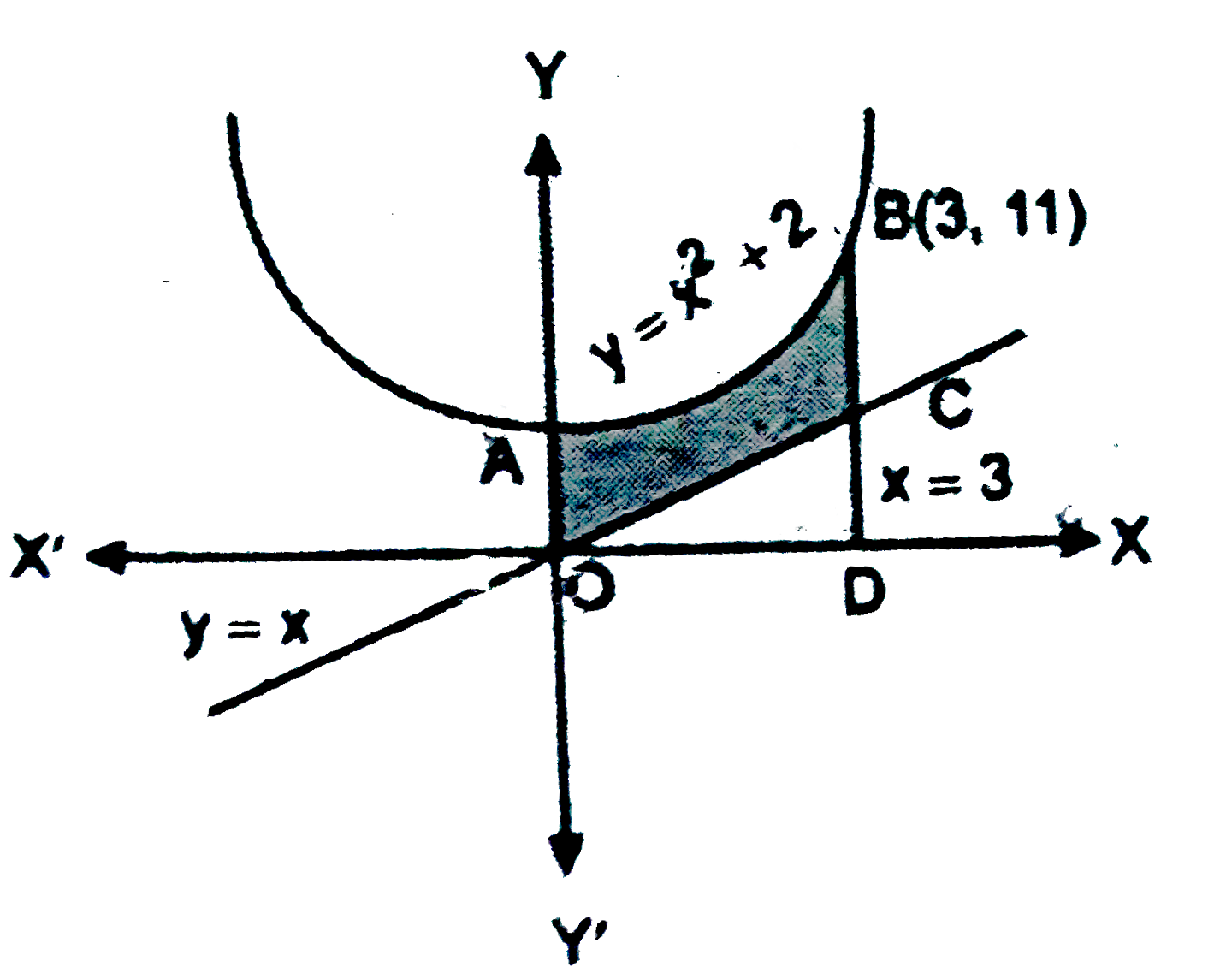
The area bounded by the curve `y=x^(2) +2, y=x,x=0` and `x=3` is represented by the shaded region.
` :. ` Required area (shaded region)
`=` area (OABDO) - area (OCDO)
`=int_(0)^(3)(x^(2)+2)dx-int_(0)^(3)xdx`
`=[(x^(3))/(3)+2x]_(0)^(3)-[(x^(2))/(2)]_(0)^(3)`
`=[(x^(3))/(3)+6-0]-[(3^(2))/(2)-0]`
`=9+6-(9)/(2)=(21)/(2)` sq. units.