Find the area of the region enclosed by y=−5x−x2andy=x on interval [−1,5]Solution in Tamil
Solving the given curves we get
5x−x2=x
∴ x2−4x=0
⇒ x=0,4
y=x(5−x) is parabola which is concave downward and intersecting x-axis at x=0 and x=5.
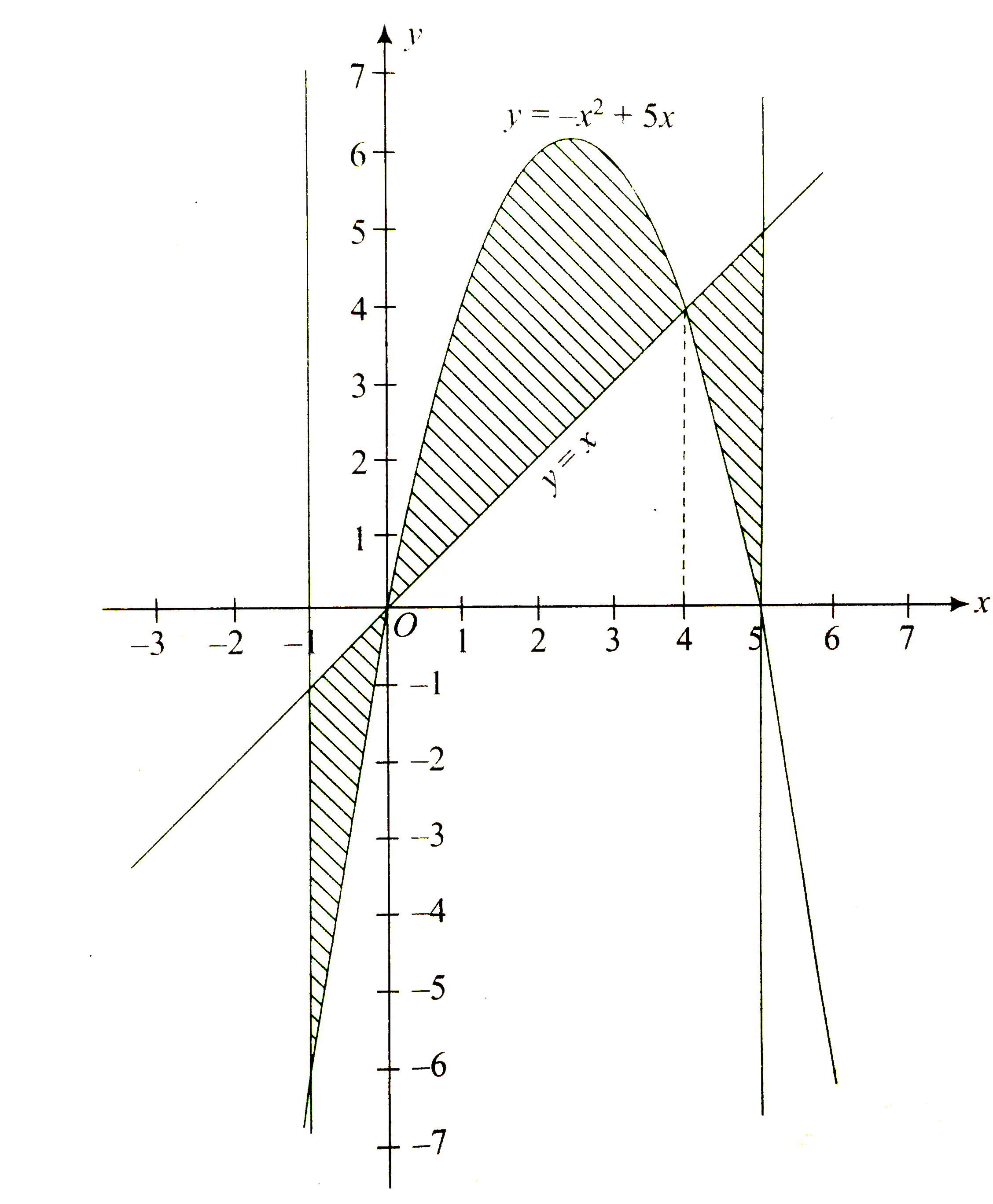
Required area, =5∫−1∣∣x−(5x−x2)∣∣dx
=5∫−1|x−4x|dx
=0∫−1(x2−4x)dx+4∫0(4x−x2)dx+5∫4(x2−4x)dx
=[x33−2x2]0−1+[2x2−x33]40+[x33−2x2]
=−[−13−2]+[32−643]+[1253−50]−[643−32]
=16−23
463 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionThe area of the region enclosed by y=x^(2) and y=sqrt(|x|) is
View SolutionFind the area of the region enclosed by y=−5x−x2andy=x on interval [−1,5]
View Solutionपरवलय y=x2 एव y=|x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionवक्रो {(x,y):x2+y2≤1≤x+y} से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutiony2=4ax तथा x2=y से घिरे क्षेत्र का क्षेत्रफल ज्ञात करें।
View SolutionDraw the rough sketch of the smaller region enclosed by the curve x2+y2=a2 and the line y = x and find the area of the enclosed region.
View SolutionFind the area of the region enclosed by the curves
y=x2 and y = 2x
View SolutionThe area of the region enclosed by the curves y=x2 and y=x3 is
View SolutionFind the area of the region enclosed by y=−5x−x2andy=x on interval [−1,5]
View SolutionThe area of the region enclosed by y=x2andy=√|x| is
View SolutionFind the area of the region enclosed by the curves
y=x2andy=√x
View Solution
