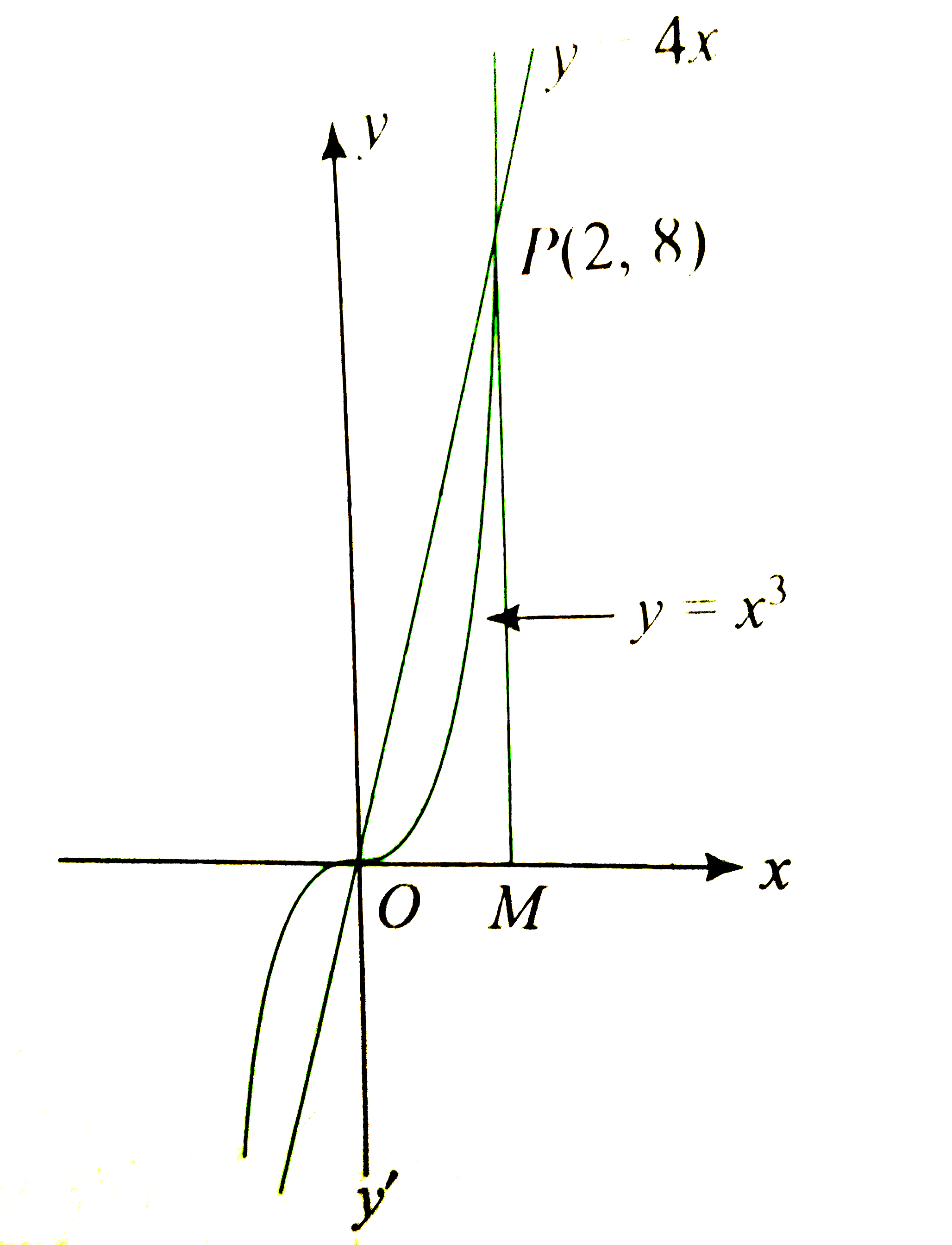
Find the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.Solution in Tamil
The correct Answer is:4 sq. units
The line y=4x meets y=x3 at 4x=x3.
∴ x=0,2,−2⇒y=0,8,−8
⇒ A=∫20(4x−x3)=(2x2−x44)20=4 sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)40videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
05:26View SolutionArea enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2isequa<o πsq.units (b) π2sq.units 3π4sq.units (d) 3π2sq.units
03:59View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
05:26View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
02:13View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
05:41View SolutionFind the area lying in the first quadrant and bounded by the curve y=x^(3) and the line y=4x.
08:31View SolutionThe area bounded by the curves y=sqrt(x),2y-x+3=0, X-axis and lying in the first quadrant is
06:08View SolutionFind the area lying in the first quadrant, bounded by the curves y2−x+2=0 and y=|x−2|.
02:36View SolutionFind the area of the region bounded by the curve x2=16y, lines y=2,y=6 and Y - axis lying in the first quadrant.
03:41View SolutionThe area (in square units) bounded by the curves : y=sqrtx, 2y-x +3 =0 x-axis , and lying in the first quadrant is :
02:35View SolutionFind the area of the region bounded by the curve y2=4x and the lines x = 1 and x = 4 lying in the first quadrant.
02:28View SolutionThe area bounded by the curves y=√x,2y−x+3=0, x-axis and lying in the first quadrant is
04:45View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
05:20View SolutionThe area of the region lying in the first quadrant and bounded by the curve y=4x2, and the lines y =2 and y =4 is "___________"
04:34View SolutionThe area of the region bounded by the curve y2=xand the Y axis in the first quadrant and lines y=3andy=9 is ______
03:35View Solution

