Find the area of the region in the first quadrant enclosed by x-axis, line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4$ .

Video Solution

Text Solution

Verified by Experts

$x^{2} + y^{2} = 4$ is the equation of a circle whose centre is (0, 0) and radius is 2. On solving the equation of circle to the straight line $x = \sqrt{3} y$ we obtained the points of intersection $A (\sqrt{3}, 1)$ and $D (- \sqrt{3}, - 1)$ .

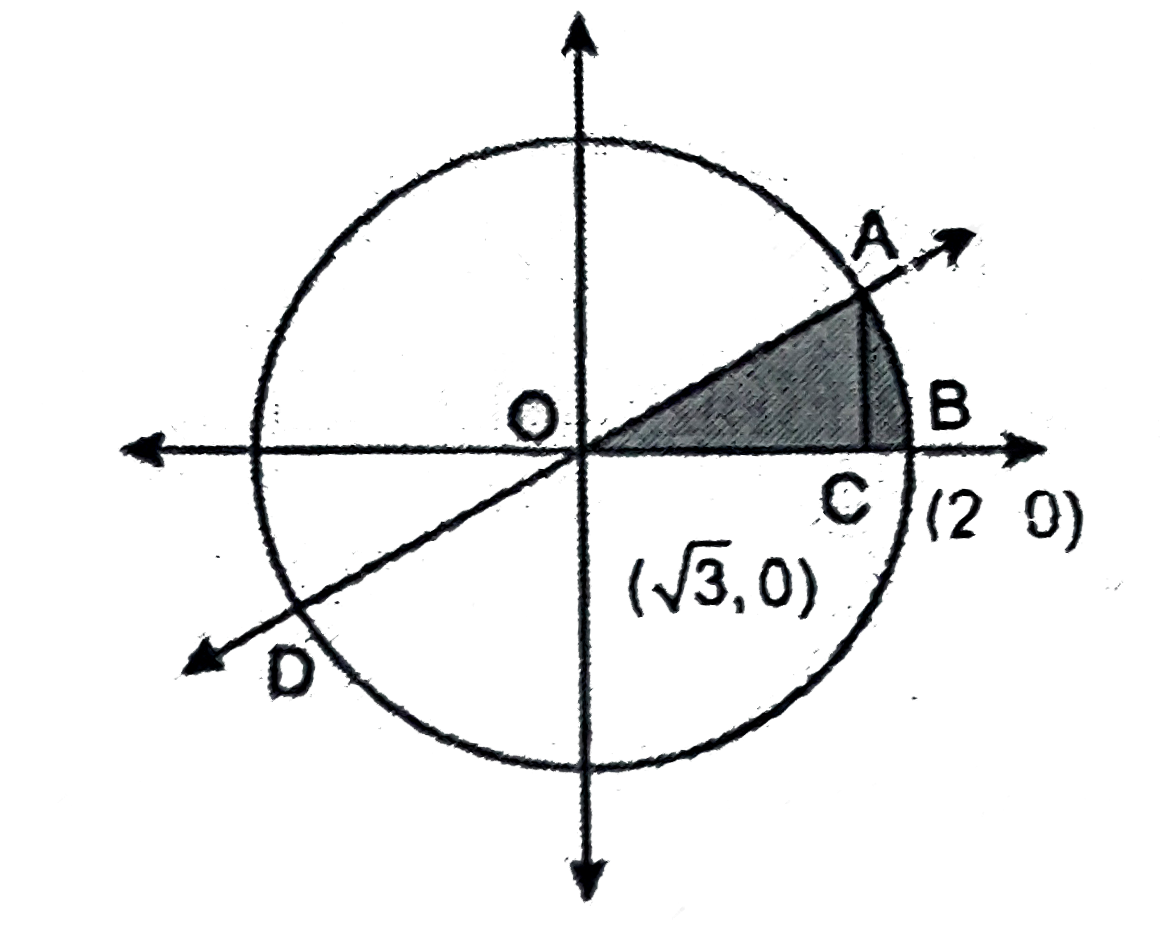
Now required area
$=$ area of OACO + area of CABC
$= \int_{0}^{\sqrt{3}} \frac{x}{\sqrt{3}} d x + \int_{\sqrt{3}}^{2} \sqrt{4 - x^{2}} d x$
$= {[\frac{x^{2}}{2 \sqrt{3}}]}_{0}^{\sqrt{3}} + {[\frac{x}{2} \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x}{2}]}_{\sqrt{3}}^{- 1}$
$= \frac{\sqrt{3}}{2} + [(0 + 2 {sin}^{- 1} 1) - (\frac{\sqrt{3}}{2} + 2 {sin}^{- 1} \frac{\sqrt{3}}{2})]$
$= \frac{\sqrt{3}}{2} + 2 \cdot \frac{π}{2} - \frac{\sqrt{3}}{2} - 2 \cdot \frac{π}{3}$
$= \frac{π}{3}$ sq. units.

Conside the line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4$
What is the area of the region in the first quadrant enclosed by the X-axis, the line $= \sqrt{3} y$ and the circle?
A $\frac{π}{3}$
B $\frac{π}{6}$
C $\frac{π}{3} - \frac{\sqrt{3}}{2}$
DNone of the above
Find the area of region in the first quadrant enclosed the X-axis, the line y =x and the circle $x^{2} + y^{2} = 32$ .
A $4 π$ sq units
B $3 π$ sq units
C $5 π$ sq units
DNone of these
Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle $x^{2} + y^{2} = 32$ is
A $16 π sq units$
B $4 π sq units$
C $32 π sq units$
D $24 π sq units$