Question

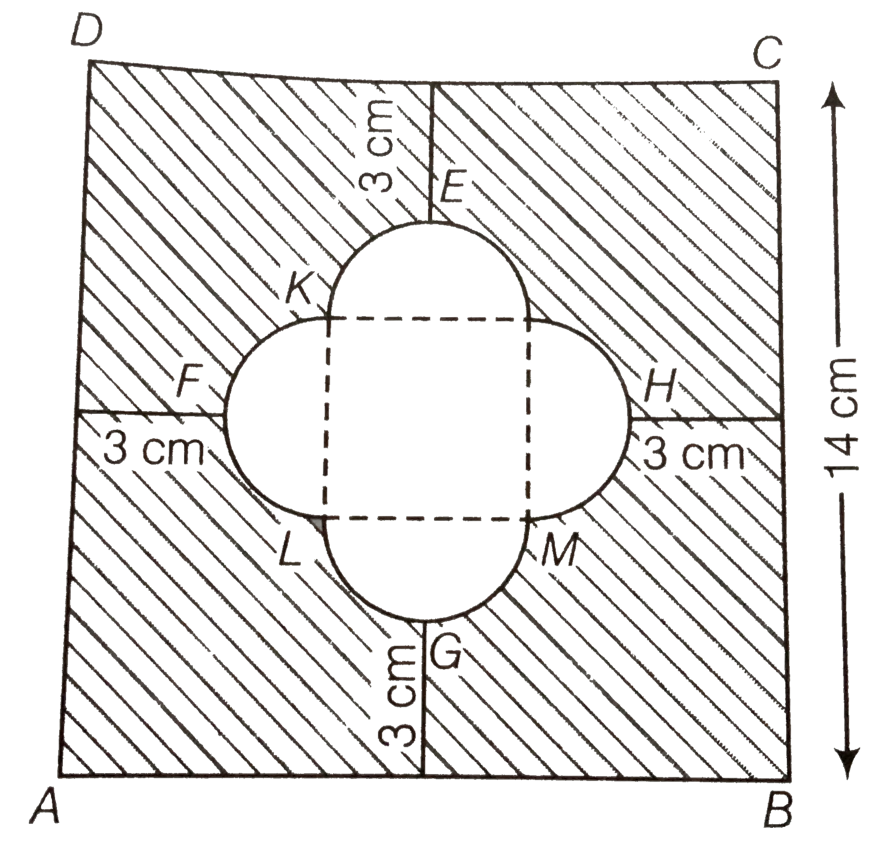
Find the area of the shaded region given in Fig. 12.72, where ABCD is a square of side 14cm.

Answer

Area of shaded region = 42.16 cm^2

Explanation

To find the area of the shaded region in the given figure where ABCD is a square of side 14 cm, we will follow these steps:

Step 1: Calculate the area of the square ABCD.
The formula for the area of a square is given by:
\( \text{Area of square} = \text{side} \times \text{side} \)
Given that the side of the square ABCD is 14 cm, we can calculate:
\( \text{Area of square} = 14 \, \text{cm} \times 14 \, \text{cm} = 196 \, \text{cm}^2 \)

Step 2: Determine the diameter and radius of the circles.
From the problem, we know that the diameter of each circle is equal to half the side of the square. Since the side of the square is 14 cm:
\( \text{Diameter of each circle} = \frac{14 \, \text{cm}}{2} = 7 \, \text{cm} \)
Now, the radius \( r \) of each circle is half of the diameter:
\( \text{Radius} = \frac{7 \, \text{cm}}{2} = 3.5 \, \text{cm} \)

Step 3: Calculate the area of one circle.
The formula for the area of a circle is:
\( \text{Area of circle} = \pi r^2 \)
Using \( \pi \approx 3.14 \) and \( r = 3.5 \, \text{cm} \):
\( \text{Area of one circle} = 3.14 \times (3.5 \, \text{cm})^2 = 3.14 \times 12.25 \, \text{cm}^2 \approx 38.46 \, \text{cm}^2 \)

Step 4: Calculate the area of four circles.
Since there are four circles in the figure, we multiply the area of one circle by 4:
\( \text{Area of four circles} = 4 \times 38.46 \, \text{cm}^2 = 153.84 \, \text{cm}^2 \)

Step 5: Calculate the area of the shaded region.
The area of the shaded region can be found by subtracting the area of the four circles from the area of the square:
\( \text{Area of shaded region} = \text{Area of square} - \text{Area of four circles} \)
Substituting the values we calculated:
\( \text{Area of shaded region} = 196 \, \text{cm}^2 - 153.84 \, \text{cm}^2 = 42.16 \, \text{cm}^2 \)

Thus, the area of the shaded region is:
\( \boxed{42.16 \, \text{cm}^2} \)