Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘
To find the area of the shaded region between two concentric circles with radii 7 cm and 14 cm, and an angle of 40∘ at the center, we will follow these steps:
Step 1: Calculate the area of the sector AOC
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
For sector AOC:
- Radius r1=7 cm
- Angle θ=40∘
Substituting the values:
Area of sector AOC=40360×π×(7)2
=19×π×49
=49π9 cm2
Step 2: Calculate the area of the sector BOD
For sector BOD:
- Radius r2=14 cm
- Angle θ=40∘
Substituting the values:
Area of sector BOD=40360×π×(14)2
=19×π×196
=196π9 cm2
Step 3: Calculate the area of the shaded region
The shaded region is the area of sector BOD minus the area of sector AOC:
Area of shaded region=Area of sector BOD−Area of sector AOC
=196π9−49π9
=196π−49π9
=147π9 cm2
Final Answer
The area of the shaded region is:
147π9 cm2≈51.33 cm2 (using π≈3.14)
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
- Radius r1=7 cm
- Angle θ=40∘
Area of sector AOC=40360×π×(7)2
=19×π×49
=49π9 cm2
For sector BOD:
- Radius r2=14 cm
- Angle θ=40∘
Area of sector BOD=40360×π×(14)2
=19×π×196
=196π9 cm2
The shaded region is the area of sector BOD minus the area of sector AOC:
Area of shaded region=Area of sector BOD−Area of sector AOC
=196π9−49π9
=196π−49π9
=147π9 cm2
The area of the shaded region is:
147π9 cm2≈51.33 cm2 (using π≈3.14)
Similar Questions
Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘
View SolutionFind the area of the shaded region in Fig. 15.29, where radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40o . (FIGURE)
View SolutionFind the area of the shaded region in the figure given below where radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘.
 View Solution
View SolutionFind the area of the shaded region in Fig. 12.19, if PQ=24 cm, PR=7 cm and O is the centre of the circle.
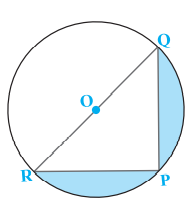 View Solution
View SolutionFind the area of the shaded region in Fig where ABCD is a square of side 14 cm.
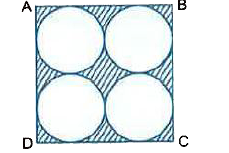 View Solution
View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View SolutionFind the area of the shaded region in Fig. 8, where APD, AQB, BRC and CSD are semi-circles of diameter 14 cm, 3.5 cm, 7 cm and 3.5 cm respectively.
View SolutionFind the area of the shaded region in Fig. 12.56, if AC= 24 cm, BC= 10 cm and O is the centre of the circle. (π=3.14)
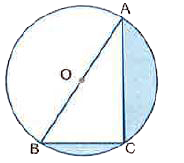 View Solution
View SolutionFind the area of the shaded region, if the diameter of the circle with centre O is 28 cm and AQ=14AB [Use π=227]
View SolutionFind the area of shaded portion given that the circles with centers O and O' are 6 cm and 18 cm in diameter respectively and ACB is a semi circle.
 View Solution
View Solution

