Find the coefficient of x5 in the expansioin of the product (1+2x)6(1−x)7.
Video Solution
Text Solution
We know that
(a+b)n=nC0an+nC1an−1b1+........+nCn−1a1bn−1+nCnbn
Hence,
(a+b)6=6C0a6+6C1a5b1+6C2a4b2+6C3a3b3+6C4a2b4+6C5a1b5+6C6b6
=a6+6!1!(6−1)!a5b1+6!2!(6−2)!a4b2+6!3!(6−3)!a3b3+6!4!(6−4)!a2b4+6!5!(6−5)!a1b5+b6
=a6+6!1×5!a5b1+6!2!×4!a4b2+6!3!3!a3b3+6!4!2!a2b4+6!5!×1a1b5+b6
=a6+6×5!5!a5b1+6×5×4!2×4!a4b2+6×5×4×3!3×2×1×3!a3b3+6×5×4!4!×2×1a2b4+6×5!5!a1b5+b6
=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6
Putting a=1 & b=2x
(1+2x)6=16+6(1)5(2x)+15(1)4(2x)2+20(1)3(2x)3+15(1)2(2x)4+6(1)(2x)5+(2x)6
=1+6(2x)+15(4x2)+20(8x3)+15(16x4)+6(32x5)+64x6
=1+12x+60x2+160x3+240x4+192x5+64x6
Similarly,
We know that
(a+b)n=nC0an+nC1an−1b1+........+nCn−1a1bn−1+nCnbn
Hence,
(a+b)7=7C0a7+7C1a6b1+7C2a5b2+7C3a4b3+7C4a3b4+7C5a2b5+7C5a1b6+7C6b7
=a7+7!1!(7−1)!a6b1+7!2!(7−2)!a5b2+7!3!(7−3)!a4b3+7!4!(7−4)!a3b4+7!5!(7−5)!a2b5+7!5!(7−6)!a1b6+b7
=a7+7!1×6!a6b1+7!2!×5!a5b2+7!3!4!a4b3+7!4!3!a3b4+7!5!×2!a2b5+7!6!×1!a1b6+b7
=a7+7×6!6!a6b1+7×6×5!2×5!a5b2+7×6×5×4!3×2×1×4!a4b3+7×6×5×4!4!×3×2×1a3b4+7×6×5!5!×2a2b5+7×6!6!a1b6+b7
=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7
Putting a=1 & b=−x
(1−x)7=(1)7+7(1)6(−x)1+21(1)5(−x)2+35(1)4(−x)3+35(1)3(−x)4+21(1)2(−x)5+7(1)(−x)6+(−x)7
=1−7x+21x2−35x3+35x4−21x5+7x6−x7
Now,
(1+2x)6(1−x)7=(1+12x+60x2+160x3+240x4+192x5+64x6)×(1−7x+21x2−35x3+35x4−21x5+7x6−x7)
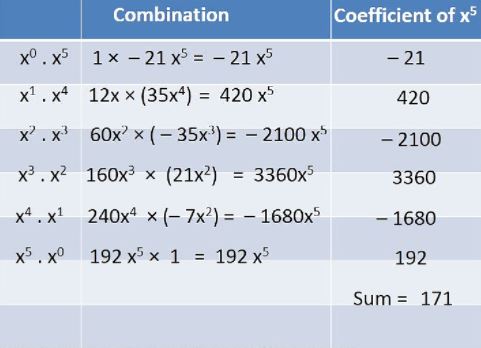
Coefficient of x5 is 171
|
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - NCERTCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 8.2
6 Videos
- BINOMIAL THEOREMBOOK - NCERTCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 8.1
14 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - NCERTCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5.4
6 Videos
Similar Questions
Knowledge Check
The coefficient of x2 in the expansion of the product (2−x2)(1+2x+3x2)6+(1−4x2)6) is:
A107B106C108D155The coefficient of x2 in the expansion of the product (2−x2).((1+2x+3x2)6+(1−4x2)6) is
A106B107C155D108
Find the coefficient of x7 in the expansion of (x2+1/x)11.
View SolutionFind the coefficient of x7 in the expansion of (3x2+15x)11
View SolutionFind the coefficient of x7 in the expansion of (x−1x2)40.
View SolutionThe coefficient of x3 in the expansion of (1+2x)6(1−x)7 is
View SolutionFind the coefficient of x in the expansion of (1−3x+7x2)(1−x)16.
View SolutionFind the coefficient of x in the expansion of (1−3x+7x2)(1−x)16.
View Solution