Find the distance between the points : (a−b,b−a),(a+b,a+b)
To find the distance between the points P(a−b,b−a) and Q(a+b,a+b), we will use the distance formula. The distance d between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
Step 1: Identify the coordinates
Let:
- P=(x1,y1)=(a−b,b−a)
- Q=(x2,y2)=(a+b,a+b)
Step 2: Substitute the coordinates into the distance formula
Now, we substitute the coordinates into the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting x1, y1, x2, and y2:
d=√((a+b)−(a−b))2+((a+b)−(b−a))2
Step 3: Simplify the expressions
Now, simplify the expressions inside the square root:
1. For (x2−x1):
(a+b)−(a−b)=a+b−a+b=2b
2. For (y2−y1):
(a+b)−(b−a)=a+b−b+a=2a
Step 4: Substitute back into the distance formula
Now substitute these simplified expressions back into the distance formula:
d=√(2b)2+(2a)2
Step 5: Calculate the squares
Calculating the squares gives:
d=√4b2+4a2
Step 6: Factor out the common term
Factor out the common term:
d=√4(a2+b2)=2√a2+b2
Final Answer
Thus, the distance between the points P and Q is:
d=2√a2+b2
Let:
- P=(x1,y1)=(a−b,b−a)
- Q=(x2,y2)=(a+b,a+b)
Now, we substitute the coordinates into the distance formula:
Now, simplify the expressions inside the square root:
(a+b)−(a−b)=a+b−a+b=2b
(a+b)−(b−a)=a+b−b+a=2a
Now substitute these simplified expressions back into the distance formula:
Calculating the squares gives:
Factor out the common term:
Thus, the distance between the points P and Q is:
Similar Questions
Find the distance between the points (a,b)and(−b,a)
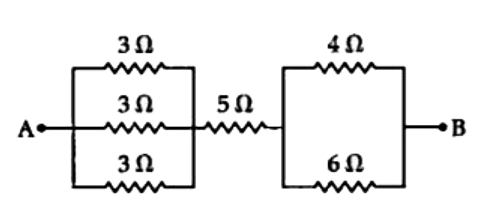
View SolutionFind the resistance between points A and B.
View SolutionFind distance between the points A (a,b) and B( - b,a)
View SolutionFind the distance between origin and the point (a, -b).
View SolutionFind the distance between the points A(3,2,1), B(-1,2,-3).
View SolutionFind the equation to the straight line which bisects the distance between the points (a,b), (a′,b') and also bisects the distance between the points (−a,b)and (a′,−b′).
View SolutionFind the distance between the points A(-2,1,3) and B(1,2,6).
View SolutionFind the distance between the points: (i)P(−6,7) andQ(−1,−5) (ii)R(a+b,a−b) and S(a−b,−a−b) (iii)A(at1,2at1) and B(at2,2at2)
View SolutionFind the distance between points A(4,6) and B(4,−2) .
View SolutionThe distance between the points A(0,6) and B(0,-2) is
View Solution
