Find the distance of each of the following points from the corresponding given plane: (2,3,−5),x+2y−2z=9
To find the distance of the point (2,3,−5) from the plane given by the equation x+2y−2z=9, we can use the formula for the distance d from a point (x1,y1,z1) to a plane given by the equation Ax+By+Cz+D=0:
d=|Ax1+By1+Cz1+D|√A2+B2+C2
Step 1: Identify the coefficients from the plane equation
The given plane equation is:
x+2y−2z=9
We can rewrite this in the standard form Ax+By+Cz+D=0:
x+2y−2z−9=0
From this, we can identify:
- A=1
- B=2
- C=−2
- D=−9
Step 2: Substitute the point coordinates into the formula
The coordinates of the point are (x1,y1,z1)=(2,3,−5).
Now substitute x1,y1,z1 into the distance formula:
d=|1(2)+2(3)+(−2)(−5)−9|√12+22+(−2)2
Step 3: Calculate the numerator
Now calculate the numerator:
1(2)+2(3)+(−2)(−5)−9=2+6+10−9
Calculating this step-by-step:
- 2+6=8
- 8+10=18
- 18−9=9
Thus, the numerator becomes:
|9|=9
Step 4: Calculate the denominator
Now calculate the denominator:
√12+22+(−2)2=√1+4+4=√9=3
Step 5: Calculate the distance
Now, substitute the values back into the distance formula:
d=93=3
Final Answer
The distance of the point (2,3,−5) from the plane x+2y−2z=9 is 3.
---
The given plane equation is:
- A=1
- B=2
- C=−2
- D=−9
The coordinates of the point are (x1,y1,z1)=(2,3,−5).
Now calculate the numerator:
- 8+10=18
- 18−9=9
Now calculate the denominator:
Now, substitute the values back into the distance formula:
The distance of the point (2,3,−5) from the plane x+2y−2z=9 is 3.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 11 F
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 11 G
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 11 D
35 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
- VECTORSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VECTORSEXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
Find the distance of each of the following points from the corresponding given plane: (3,−2,1),(2x−y+2z+3=0
View SolutionFind the distance of each of the following points from the corresponding given plane: (−6,0,0),2x−3y+6z−2=0
View SolutionFind the distance of each of the following points from the corresponding given plane: (0,0,0),3x−4y+12z=3
View SolutionIn the following cases, find the distance of each of the given points from the corresponding given plane. Point Plane(a) (0,0,0) 3x−4y+12z=3 (b) (3,−2,1) 2xy+2z+3=0 (c) (2,3,−5) x+2y−2z=9 (d)(−6,0,0) 2x−3y+6z−2=0
View SolutionIn the following cases, find the distance of each of the given points from the corresponding given plane.
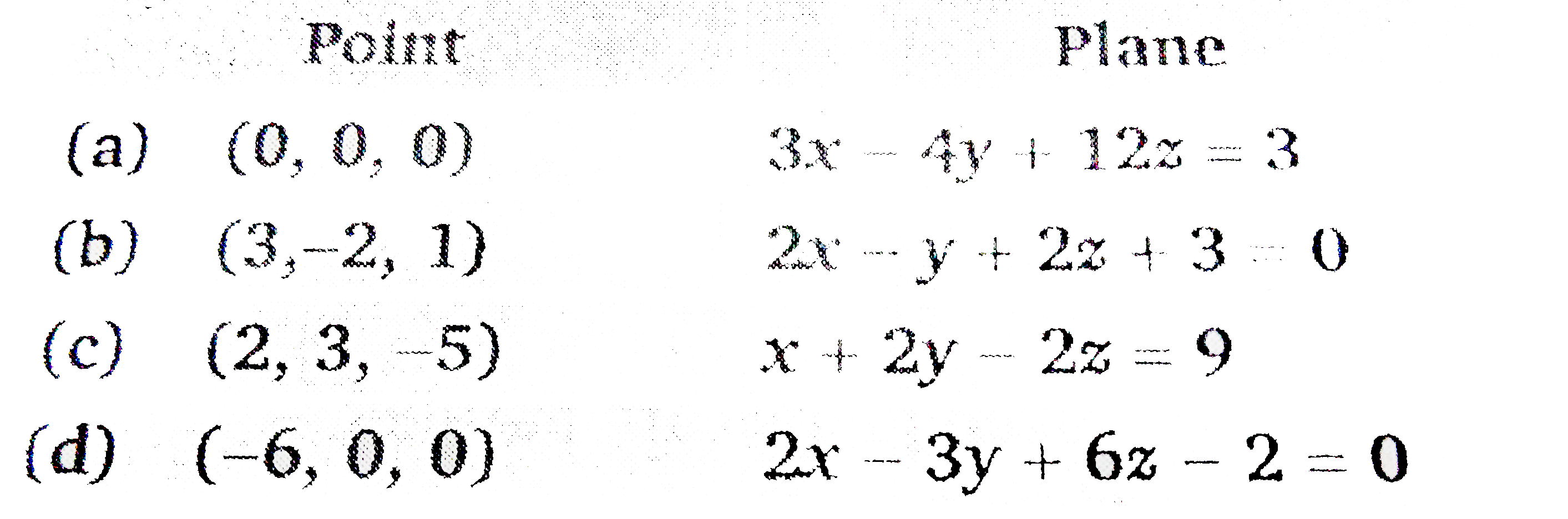
View SolutionFind the distance of the plane 2x−y−2z−9=0 from the origin.
View SolutionFind the distance of the point (21,0) from the plane 2x+y+2z+5=0.
View SolutionFind the distance of the point (1,2,0) from the plane 4x+3y+12z+16=0
View SolutionFind the distance of the point (2, 3, -5) from the plane x+2y−2z−9=0.
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View Solution
