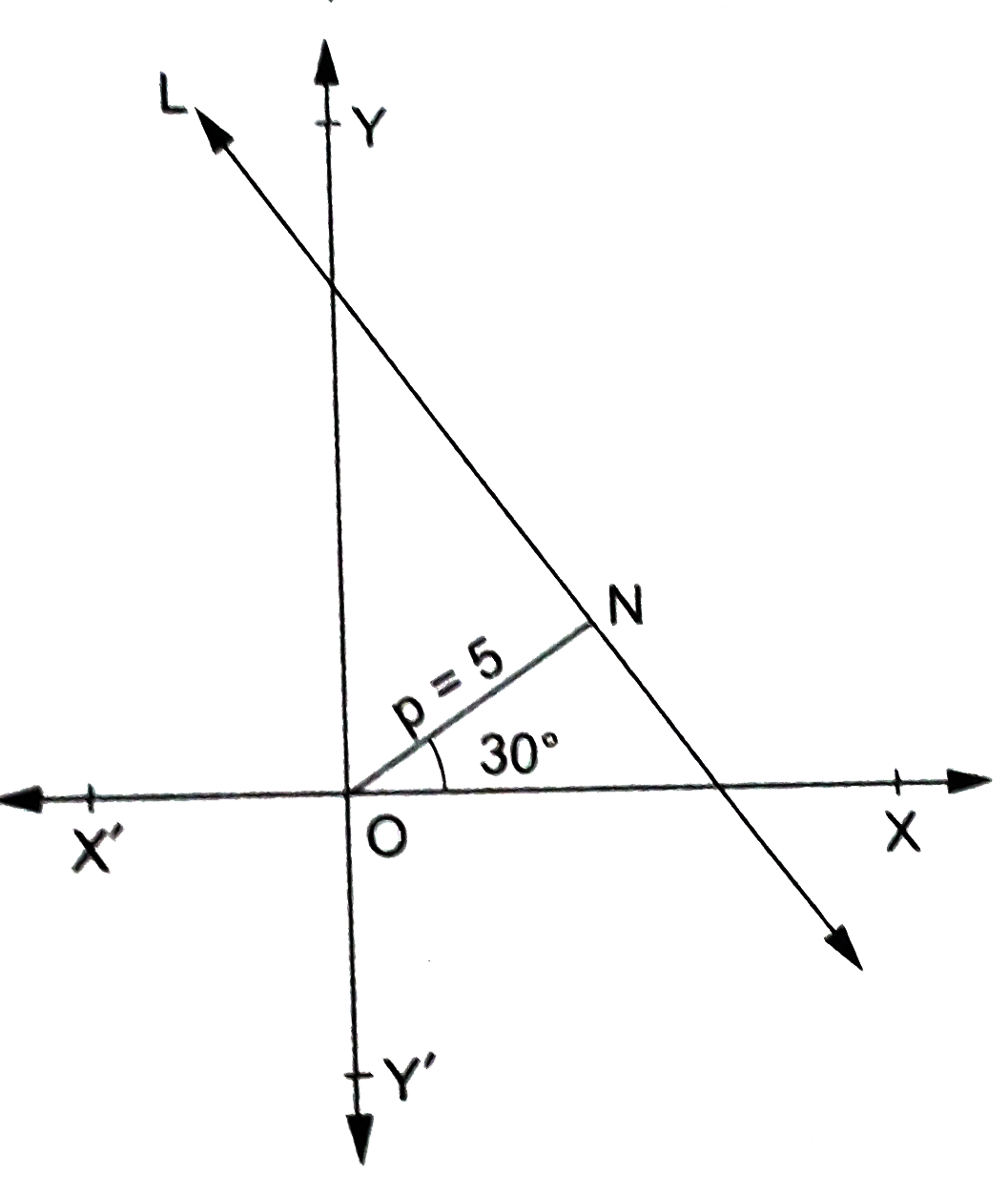
Find the equation of a line which is at a distance of $5$ units from origin and the perpendicular from origin to this line makes an angle of $30^{\circ}$ from the positive direction of $X$ -axis.

Video Solution

Text Solution

Verified by Experts

Here p=5 units and $α = 30^{\circ}$
So, the equation of the given line in normal form is
$x cos α + y sin α = p, where α = 30^{\circ} and p = 5 units$

$\Leftrightarrow x {cos 30}^{\circ} + y {sin 30}^{\circ} = 5$
$\Leftrightarrow x (\frac{\sqrt{3}}{2}) + y (\frac{1}{2}) = 5$
$\Leftrightarrow \sqrt{3} x + y - 10 = 0$

Updated on:21/07/2023