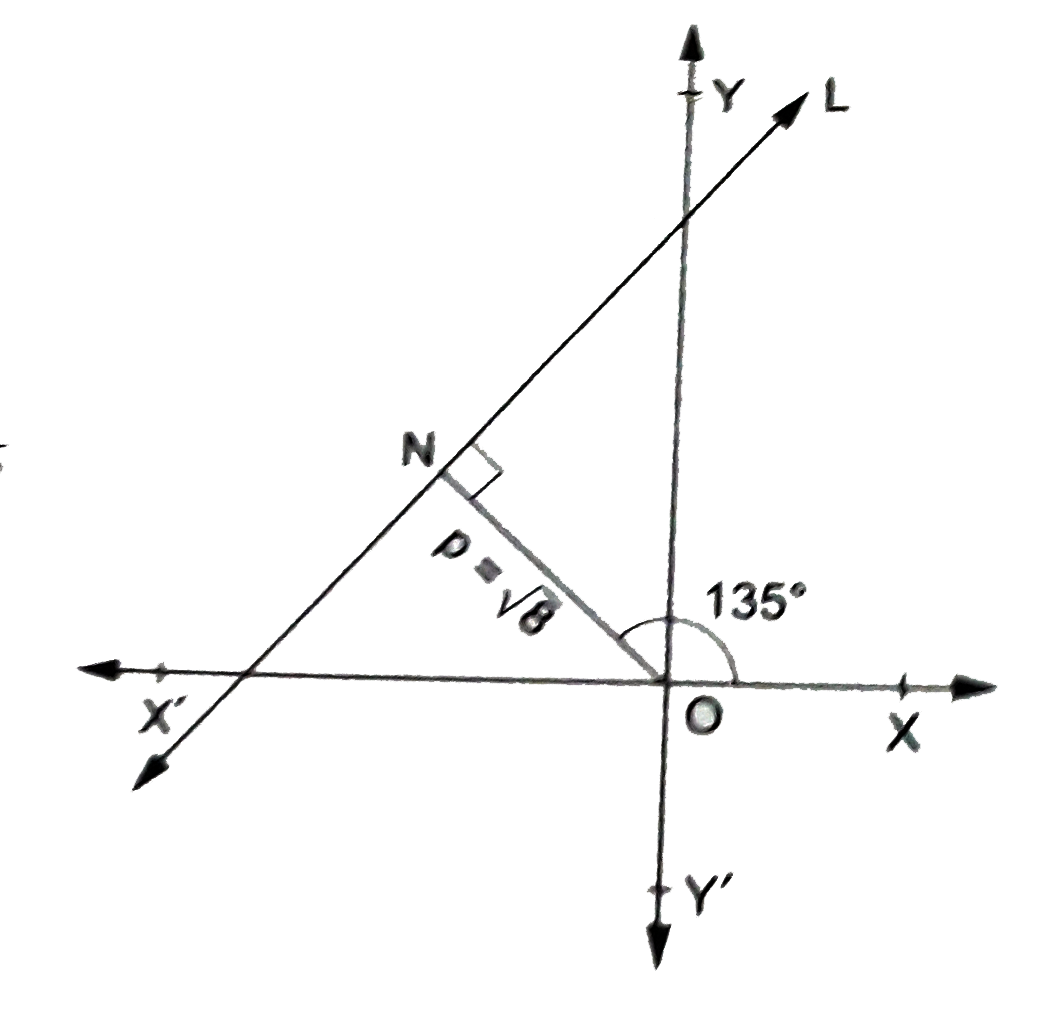
Find the equation of a line whose perpendicular disatnce from the origin is √8 units and the angle between the positive direction of the x-axis and the perpendicular is 135∘ .
Here p=√8 units are α=135∘
So, the equation of the given line in normal form is
xcosα+ysinα=p
where α=135∘andp=√8units
⇔xcos135∘+ysin135∘=√8
⇔xcos135∘+ysin135∘=√8
⇔x(−1√2)+y(1√2)=√18
[∴cos135∘=cos(180∘−45∘)=−cos45∘sin135∘=sin(180∘−45∘)=sin45∘]
−x+y=4⇔x−y+4=0, which is the required equation.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - SOLVED-EXAMPLE12videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - MISCELLANEOUS PROBLEMS9videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE 20K10videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30D5videos
STATISTICS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Find the equation of the line whose perpendicular distance from the origin is 3 units and the angle between the positive direction of x-axis and the perpendicular is 15∘.
View SolutionFind the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with the positive direction of x–axis is 15°.
View Solution
Knowledge Check
- Question 1 - Select One
The equation of the line whose perpendicular distance from the origin is 3 units and the angle which the normal makes with with the positive direction of x -axis is 30∘ is
Ax+√3y=3B√3x+y=6C√3x+y=1Dx+√3y=6
Find the equation of a line with slope −1 and whose perpendicular distance from the origin is equal to 5
View SolutionFind the equation of a line whose perpendicular distance from the origin is 2 units and the angle between the perpendicular segment and the positive of the x-axis is 240∘.
View SolutionFind the equation of the line whose perpendicular distance from origin is 5 units and the angle which the normal makes with the positive direction of x-axis is 225∘.
View SolutionFind the equation of the line whose perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive X-axis is 30∘
View SolutionFind the equation of a line with slope –1 and whose perpendicular distance from the origin is equal to 5.
View SolutionFind the points on x-axis whose perpendicular distance from the line 3x−4y−12=0 is 3.
View SolutionFind the equation of the line perpendicular to x-axis and passing through the origin.
View Solution

