Find the equation of each of the following parabola
focus at $(- 1, 2)$ directrix $x - 2 y + 3 = 0$

Video Solution

Text Solution

Verified by Experts

(i) Given that , directrix=0 and focus =(6,0)
So, the equation of the parabola
${(x - 6)}^{2} + y^{2} = x^{2}$
$\Rightarrow x^{2} + 36 - 12 x + y^{2} = x^{2}$ ltbr> $\Rightarrow y^{2} - 12 x + 36 = 0$
(ii) given that, vertex=(0,4) and focus=(0,2)

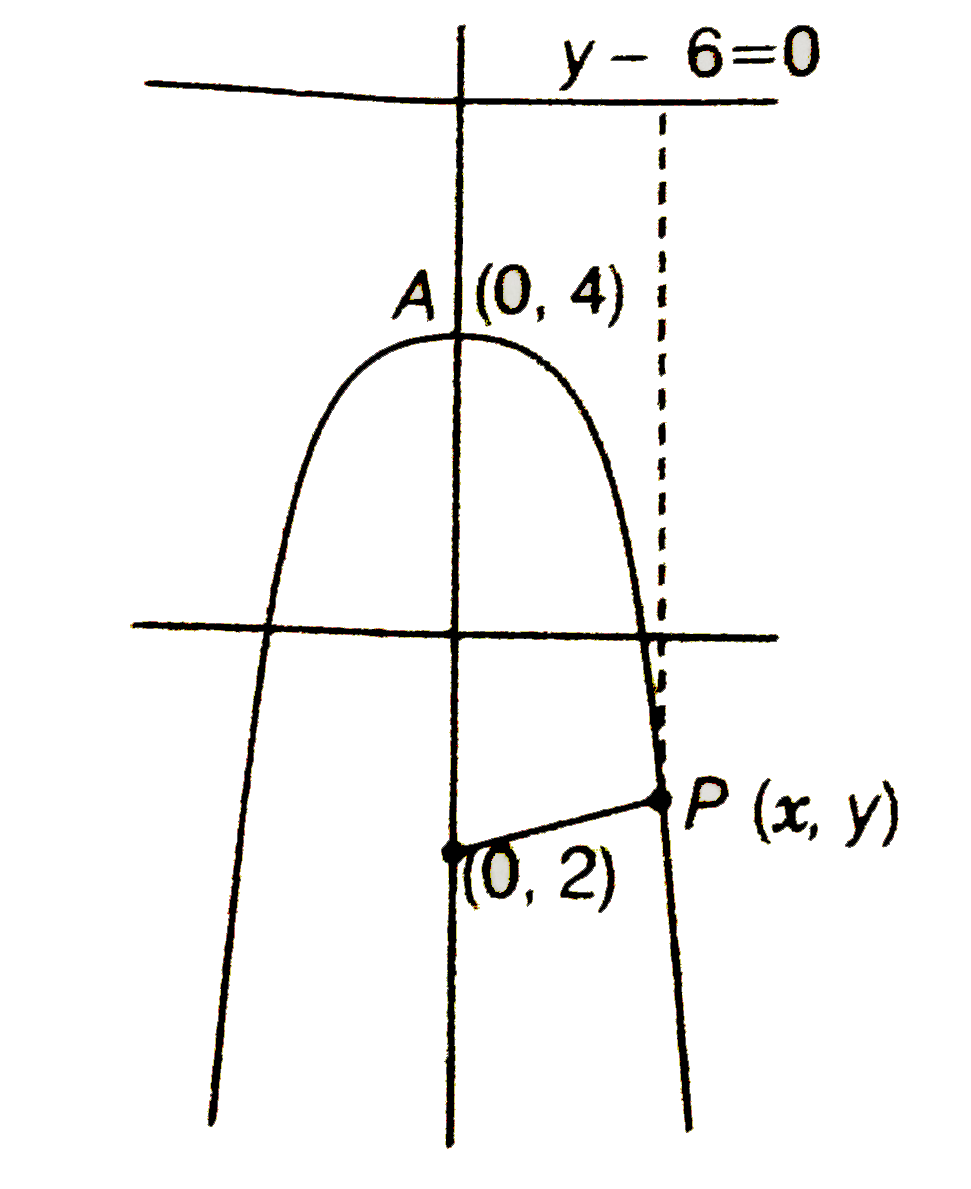
So, the equation of parabola is
$\sqrt{{(x - 0)}^{2} + {(y - 2)}^{2}} = | y - 6 |$
$\Rightarrow x^{2} + y^{2} - 4 y + 4 = y^{2} - 12 y + 36$
$\Rightarrow x^{2} - 4 y + 12 y - 32 = 0$
$\Rightarrow x^{2} + 8 y - 32 = 0$
$\Rightarrow x^{2} = 32 - 8 y$
(iii) Given that, focus at (-1,-2) and directrix x-2y+3=0
So, the equation of paarobola is $\sqrt{{(x - 1)}^{2} + {(y - 2)}^{2}} = ∣ ∣ ∣ \frac{x - 2 y + 3}{\sqrt{1 + 4}} ∣ ∣ ∣$
$\Rightarrow x^{2} + 2 x + 1 + y^{2} + 4 y + 4 = \frac{1}{5} [x^{2} + 4 y^{2} + 9 - 4 x y - 12 y + 6 x]$
$\Rightarrow 4 x^{2} + 4 x y + y^{2} + 4 x + 32 y + 16 = 0$

Updated on:21/07/2023

|

Class 11 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the equation of the parabola with focus at (3, -4) and directrix x + y - 2 = 0 .
A $x^{2} + 4 x y + y^{2} - 8 x + 20 y + 46 = 0$
B $x^{2} + 2 x y + y^{2} - 8 x + 20 y + 46 = 0$
C $x^{2} - 2 x y + y^{2} - 8 x + 20 y + 46 = 0$
D $x^{2} - 4 x y + y^{2} - 8 x + 20 y + 46 = 0$

NCERT EXEMPLAR-CONIC SECTIONS-Long answer

Home
Ask Doubt
Profile