Find the equations of straight lines which pass through the intersection of the lines x−2y−5=0,7x+y=50 & divide the circumference of the circle x2+y2=100 into two arcs whose lengths are in the ratio 2:1.Solution in Tamil
3x+4y−25=0
4x−3y−25=0
3x+2y−23=0
2x−3y−11=0
The correct Answer is:1,2
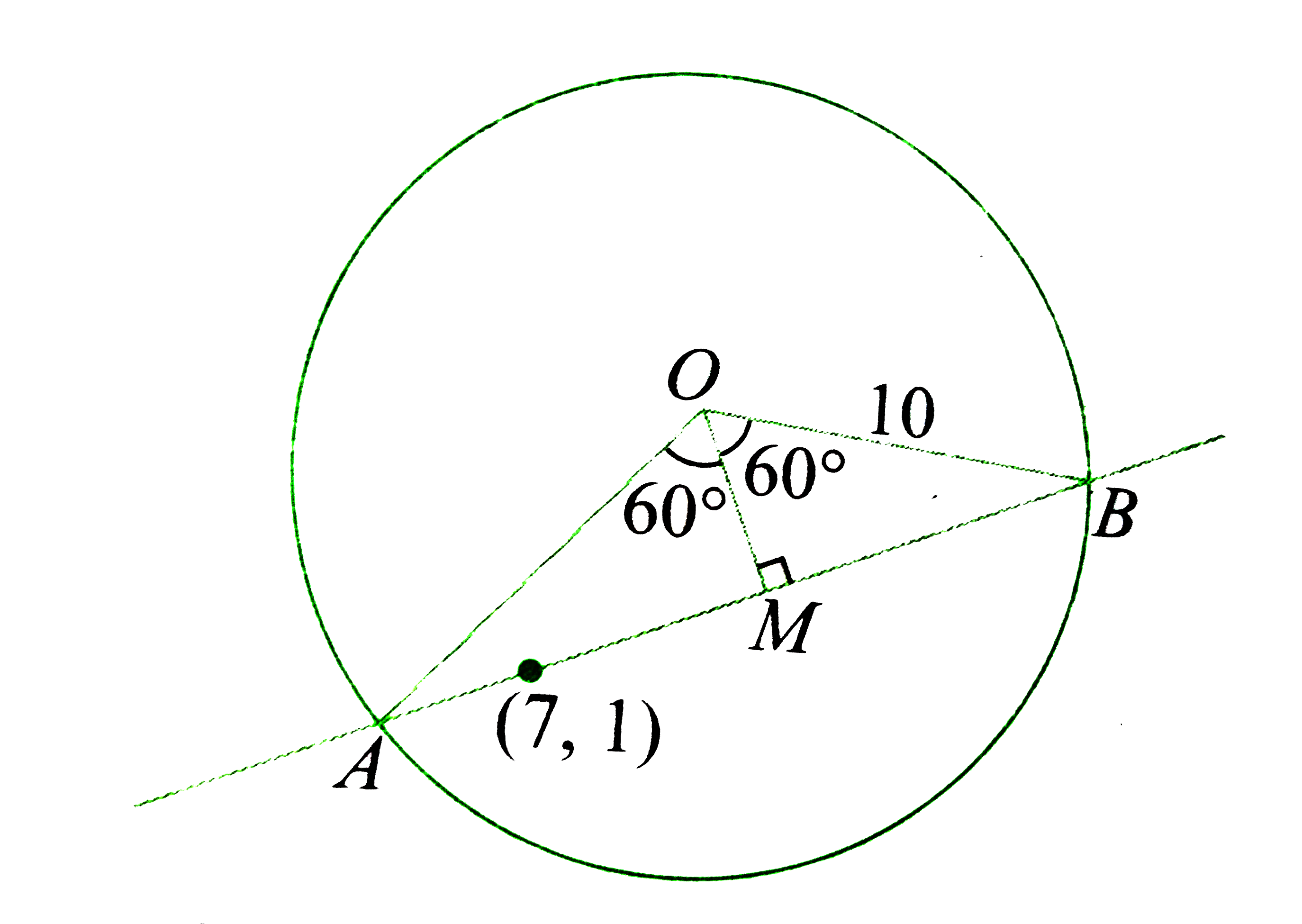
Point of intersection of given lines is (7,1), which lies inside the circle x2+y2=100
If line chord AB thought this point divides circumeference of the circle into two arcs whose lengths are in the ratio 2:1, then AB subtends an angle of 120∘ at the centre
So, from the figure, OM=10cos60∘=5
Let the equation of line through (7,1) be
y−1=m(x−7)
or mx−y−7m+1=0 (1)
OM=5
⇒∣∣∣1−7m√1+m2∣∣∣=5
⇒(1−7m)2=25(1+m2)
⇒24m2−14m−24=0
⇒(4m+3)(6m−8)=0
⇒m=−34,m=43
Putting the value of m in (i) , we get
y−1=−34(x−7) and y−1=43(x−7)
or 3x+4y−25=0 and 4x−3y−25=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Single)
109 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Each side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionLet C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
View SolutionThe number of rational point(s) [a point (a, b) is called rational, if aandb both are rational numbers] on the circumference of a circle having center (π,e) is a)at most one b) at least two c)exactly two d) infinite
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionFind the equations of straight lines which pass through the intersection of the lines x-2y-5=0,7x+y=50 divide the circumference of the circle x^(2)+y^(2)=100 into two arcs whose lengths are in the ratio 2:1.
View SolutionFind the equation of the circle passing through the intersection of the circles x^(2)+y^(2)-4=0 and x^(2)+y^(2)-2x-4y+4=0 and touching the line x+2y=0
View SolutionThe line 4x+2y+k=0 divides the circumference of the circle x^(2)+y^(2)=100 in the ratio 1:2 then the value of 'k' is
View SolutionFind the equation of the circle which bisects the circumference of the circle x2+y2+2y−3=0 and touches the straight line y = x at the origin.
View SolutionFind the equation of the straight line which passes through the centre of the circle x2+y2+2x+2y−23=0 and is perpendicular to the straight line x-y+8 = 0.
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो y−x−1=0 तथा 2x−y+1=0 के प्रतिच्छेद बिंदु से होकर जाती है तथा रेखा 3x+2y=0 पर लम्ब है
View Solutionउस वृत्त का समीकरण ज्ञात कीजिये जो सरल रेखा 2x−y+3=0 को स्पर्श करता है तथा सरल रेखा x+2y−1=0 व वृत्त x2+y2−2x+1=0 के प्रतिच्छेद बिन्दुओ से होकर गुजरता है ।
View SolutionThe angle between the chords of the circle x2+y2=100, which passes through the point (7,1) and also divides the circumference of the circle into two arcs whose length are in the ratio 2 : 1, is equal to
View Solution" The equation of smallest circle passing through intersection of curve "x2+y2−4x−2y−2=0" and line "x+y−5=0" is
View SolutionFind the equations of straight lines which pass through the intersection of the lines x−2y−5=0,7x+y=50 & divide the circumference of the circle x2+y2=100 into two arcs whose lengths are in the ratio 2:1.
View SolutionA line that x +y =2 , x -y =0 And the line passes through the intersection of x +2y =5 Is parallel to
View Solution
