Find the equations of the circles touching y-axis at (0,3) and making an intercept of 8 units on the x-axis.
x2+y2±10x−6y+9=0
x2+y2±6x−10y+9=0
x2+y2−8x±10y+9=0
x2+y2+10x±6y+9=0
The correct Answer is:A
Given equation of circle touch the Y-axis at(0,3).
In △AOB,r=√32+42=5
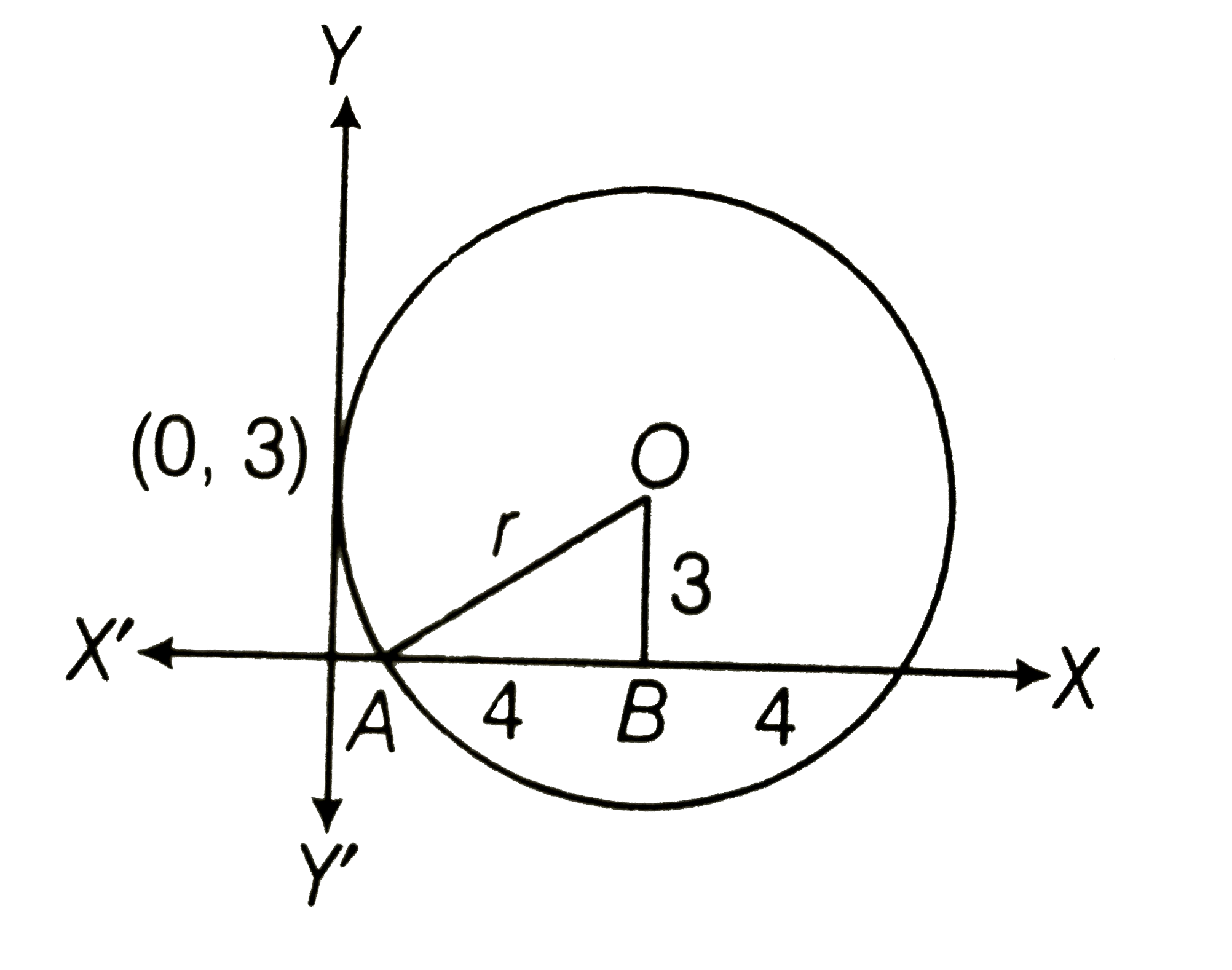
The point (0, 3) and radius 5 satisfies the equation
x2+y2±10x−6y+9=0.
Topper's Solved these Questions
Similar Questions
Centre of the circle toucing y-axis at (0,3) and making an intercept 2 units on positive X-axis is
View SolutionThe equation of the circle touching Y-axis at (0,3) and making intercept of 8 units on the axis (a) x2+y2−10x−6y−9=0 (b) x2+y2−10x−6y+9=0 (c) x2+y2+10x−6y−9=0 (d) x2+y2+10x+6y+9=0
View Solution
Knowledge Check
The equation of a circle touching x-axis at (−4,0) and cutting off an intercept of 6 units on y-axis can be
Ax2+y2+8x+12y+16=0Bx2+y2+8x−12y+16=0Cx2+y2+8x+10y+16=0Dx2+y2+8x−10y+16=0Equations of circle which touch y-axis at (0, 3) and intercepts a length of 8 units on the x-axis is
Ax2+y2+10x−6y+9=0Bx2+y2+6x−10y+9=0Cx2+y2+8x+4y+2=0Dx2+y2−10x−6y+9=0Equation of a circle which touches y-axis at (0,2) and cuts ff an intercept of 3 units from the x-axis is x2+y2−2αx−4y+4=0 where α2=
A5/2B25/4C4/25D29
Find the equations of the circles which touch Y-axis at
the point (0,3) , and make an intercept of 8 units on the X-axis .
View SolutionFind the equation of the circle touching : x-axis andhaving centre at (4, 3)
View SolutionEquation of circle which touches the axis of y at (0, 3) and cuts an intercepts of 8 units on the axis of x
View SolutionA circle touches x-axis at (2, 0) and has an intercept of 4 units on the y-axis. Find its equation.
View SolutionFind the equation of the circle touching : x-axis at the origin and having radius 10
View Solution
