Question

Find the locus of the midpoint of the chords of the circle $x^2+y^2=a^2$
which subtend a right angle at the point $(c,0)\stackrel{.}{}$

Options

A. `x^(2)+y^(2)=(a^(2))/(2)`
B. `x^(2)+y^(2)=2a^(2)`
C. `x^(2)+y^(2)=(a^(2))/(4)`
D. none of these

Answer

A

Explanation

Let (h, k) be the mid-point of a chord AB of the circle `x^(2)+y^(2)=a^(2)`. Then, the equation of AB is
`hx+ky-a^(2)=h^(2)+k^(2)-a^(2) " "`[Using T = S']
or, `hx+ky=h^(2)+k^(2) " " ...(i)`

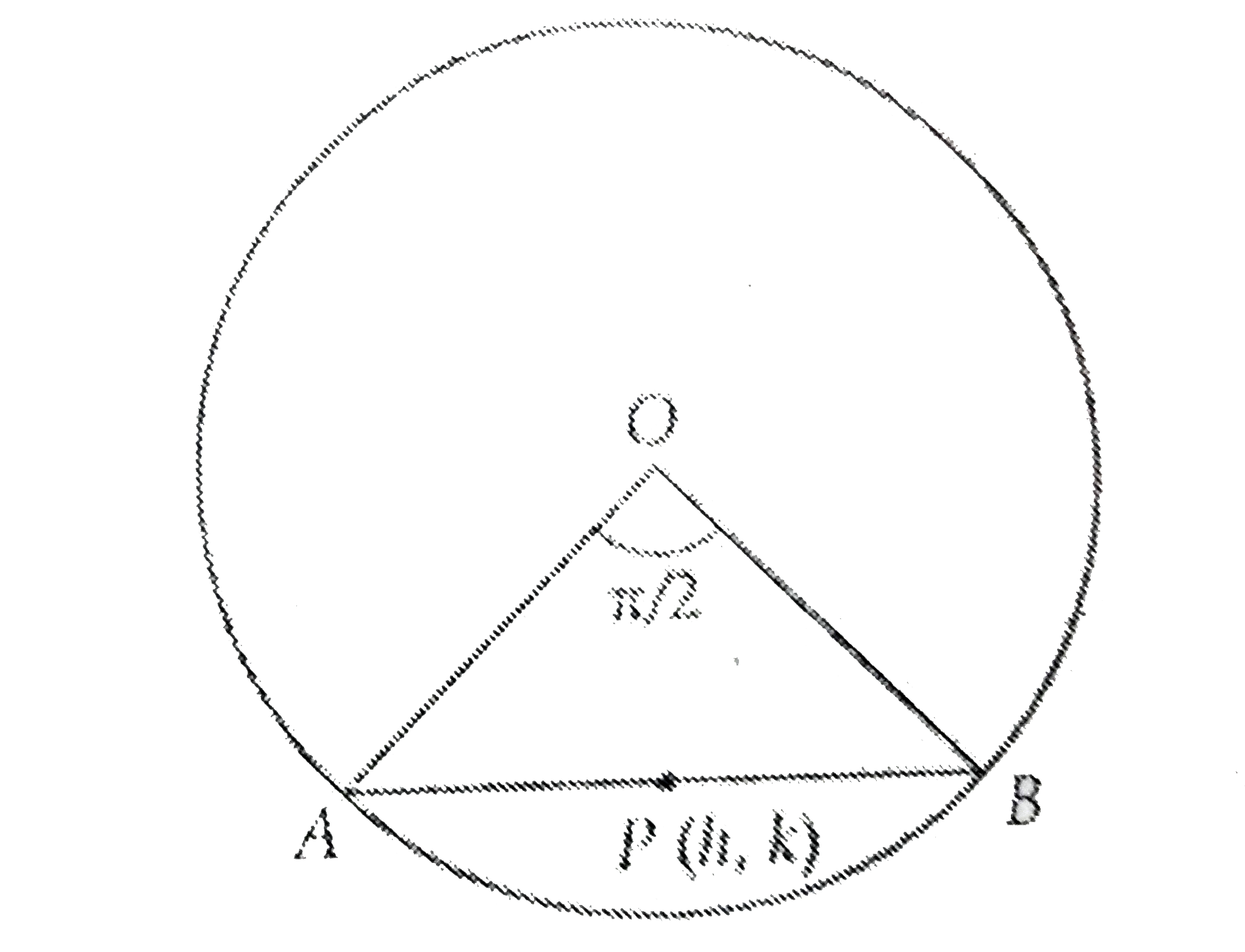
The combined equation of OA and OB is
`x^(2)+y^(2)=a^(2)((hx+ky)/(h^(2)+k^(2)))^(2)`
or, `(h^(2)+k^(2))^(2)(x^(2)+y^(2))-a^(2)(hx+ky)^(2)=0`
OA and OB will be perpendicular, if
Coeff. of `x^(2)+` Coeff. of `y^(2)=0`
`rArr (h^(2)+k^(2))^(2)-a^(2)h^(2)+(h^(2)+k^(2))^(2)-a^(2)k^(2)=0`
`rArr 2(h^(2)+k^(2))-a^(2)(h^(2)+k^(2))=0rArr 2(h^(2)+k^(2))-a^(2)=0`
So, locus of (h, k) is `2 (x^(2)+y^(2))-a^(2)=0`.