Find the matrices of transformation T1T2andT2T1 when T1 is rotated through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1.
To solve the problem, we need to find the transformation matrices T1 and T2 based on the given transformations, and then compute the products T1T2 and T2T1.
Step 1: Define the transformation matrices
1. Rotation Matrix T1:
The rotation matrix for an angle θ is given by:
T1=(cosθ−sinθsinθcosθ)
For θ=60∘:
cos60∘=12,sin60∘=√32
Therefore,
T1=⎛⎜⎝12−√32√3212⎞⎟⎠
2. Reflection Matrix T2:
The reflection in the Y-axis is given by:
T2=(−1001)
Step 2: Calculate T1T2
Now we will compute T1T2:
T1T2=⎛⎜⎝12−√32√3212⎞⎟⎠(−1001)
Performing the multiplication:
T1T2=⎛⎜⎝12⋅(−1)+(−√32)⋅012⋅0+(−√32)⋅1√32⋅(−1)+12⋅0√32⋅0+12⋅1⎞⎟⎠
This simplifies to:
T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠
Step 3: Calculate T2T1
Next, we compute T2T1:
T2T1=(−1001)⎛⎜⎝12−√32√3212⎞⎟⎠
Performing the multiplication:
T2T1=⎛⎜⎝−1⋅12+0⋅√32−1⋅(−√32)+0⋅120⋅12+1⋅√320⋅(−√32)+1⋅12⎞⎟⎠
This simplifies to:
T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
Step 4: Verify T1T2≠T2T1
Now we compare the two matrices:
T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠,T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
Clearly, the matrices are not equal since the off-diagonal elements differ.
Final Result
Thus, we have:
- T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠
- T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
And we verified that T1T2≠T2T1.
The rotation matrix for an angle θ is given by:
T1=(cosθ−sinθsinθcosθ)
For θ=60∘:
cos60∘=12,sin60∘=√32
Therefore,
T1=⎛⎜⎝12−√32√3212⎞⎟⎠
The reflection in the Y-axis is given by:
T2=(−1001)
T1T2=⎛⎜⎝12−√32√3212⎞⎟⎠(−1001)
T1T2=⎛⎜⎝12⋅(−1)+(−√32)⋅012⋅0+(−√32)⋅1√32⋅(−1)+12⋅0√32⋅0+12⋅1⎞⎟⎠
This simplifies to:
T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠
T2T1=(−1001)⎛⎜⎝12−√32√3212⎞⎟⎠
T2T1=⎛⎜⎝−1⋅12+0⋅√32−1⋅(−√32)+0⋅120⋅12+1⋅√320⋅(−√32)+1⋅12⎞⎟⎠
This simplifies to:
T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠,T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
- T1T2=⎛⎜⎝−12−√32−√3212⎞⎟⎠
- T2T1=⎛⎜⎝−12√32√3212⎞⎟⎠
Topper's Solved these Questions
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise For Session 1
9 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise For Session 2
19 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
29 Videos
Similar Questions
Here T1andT2 are
View SolutionT1andT2 in the given figure are
View SolutionFind T1andT2 in the given figure.

View Solution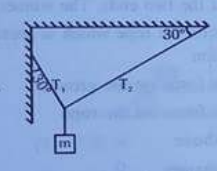
Calculate T1&T2.
View Solution
Calculate a, T1,T2,T1'&T2'.
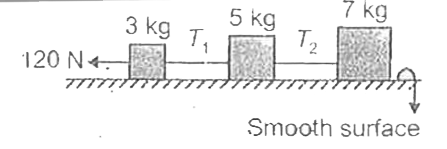
View SolutionThe surface are frictionless, the ratio of T1 and T2 is

View SolutionThe surface are frictionless, the ratio of T1 and T2 is

View SolutionFind the locus of the point (t2−t+1,t2+t+1),t∈R.
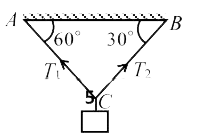
View SolutionGiven that T1=100N then find T2
View SolutionIf the tangents at t1andt2 on y2 = 4ax are at right angles if
View Solution
