Find the mean and variance of frequency distribution given below: xi: , 1≤x<3 , 3≤x<5 , 5≤x<7 , 7≤x<10 fi: , 6, 4, 5, 1
To find the mean and variance of the given frequency distribution, we will follow these steps:
Step 1: Create the Frequency Distribution Table
We have the following intervals and their corresponding frequencies:
| Interval | xi | fi |
|-------------|-----------|-----------|
| 1<x<3 | 2 | 6 |
| 3<x<5 | 4 | 4 |
| 5<x<7 | 6 | 5 |
| 7<x<10 | 8.5 | 1 |
Step 2: Calculate Mid Values
The mid value yi for each interval is calculated as follows:
- For 1<x<3: y1=1+32=2
- For 3<x<5: y2=3+52=4
- For 5<x<7: y3=5+72=6
- For 7<x<10: y4=7+102=8.5
Step 3: Calculate fiyi and fiy2i
Now, we calculate fiyi and fiy2i:
| Interval | fi | yi | fiyi | fiy2i |
|-------------|-----------|-----------|----------------|------------------|
| 1<x<3 | 6 | 2 | 6×2=12 | 6×22=24 |
| 3<x<5 | 4 | 4 | 4×4=16 | 4×42=64 |
| 5<x<7 | 5 | 6 | 5×6=30 | 5×62=180 |
| 7<x<10 | 1 | 8.5 | 1×8.5=8.5 | 1×(8.5)2=72.25 |
Step 4: Calculate Summations
Now we calculate the summations:
- Σfi=6+4+5+1=16
- Σfiyi=12+16+30+8.5=66.5
- Σfiy2i=24+64+180+72.25=340.25
Step 5: Calculate Mean
The mean ¯x is given by:
¯x=ΣfiyiΣfi=66.516=4.15625
Step 6: Calculate Variance
The variance σ2 is given by:
σ2=1nΣfiy2i−(1nΣfiyi)2
Substituting the values:
σ2=116⋅340.25−(66.516)2
Calculating:
σ2=21.265625−17.578125=3.6875
Final Results
- Mean ¯x≈4.15625
- Variance σ2≈3.6875
We have the following intervals and their corresponding frequencies:
|-------------|-----------|-----------|
| 1<x<3 | 2 | 6 |
| 3<x<5 | 4 | 4 |
| 5<x<7 | 6 | 5 |
| 7<x<10 | 8.5 | 1 |
The mid value yi for each interval is calculated as follows:
- For 1<x<3: y1=1+32=2
- For 3<x<5: y2=3+52=4
- For 5<x<7: y3=5+72=6
- For 7<x<10: y4=7+102=8.5
Now, we calculate fiyi and fiy2i:
|-------------|-----------|-----------|----------------|------------------|
| 1<x<3 | 6 | 2 | 6×2=12 | 6×22=24 |
| 3<x<5 | 4 | 4 | 4×4=16 | 4×42=64 |
| 5<x<7 | 5 | 6 | 5×6=30 | 5×62=180 |
| 7<x<10 | 1 | 8.5 | 1×8.5=8.5 | 1×(8.5)2=72.25 |
Now we calculate the summations:
- Σfi=6+4+5+1=16
- Σfiyi=12+16+30+8.5=66.5
- Σfiy2i=24+64+180+72.25=340.25
The mean ¯x is given by:
¯x=ΣfiyiΣfi=66.516=4.15625
The variance σ2 is given by:
σ2=1nΣfiy2i−(1nΣfiyi)2
Substituting the values:
σ2=116⋅340.25−(66.516)2
Calculating:
σ2=21.265625−17.578125=3.6875
- Mean ¯x≈4.15625
- Variance σ2≈3.6875
Topper's Solved these Questions
Similar Questions
Find the mean and variance for the following frequency distributions in
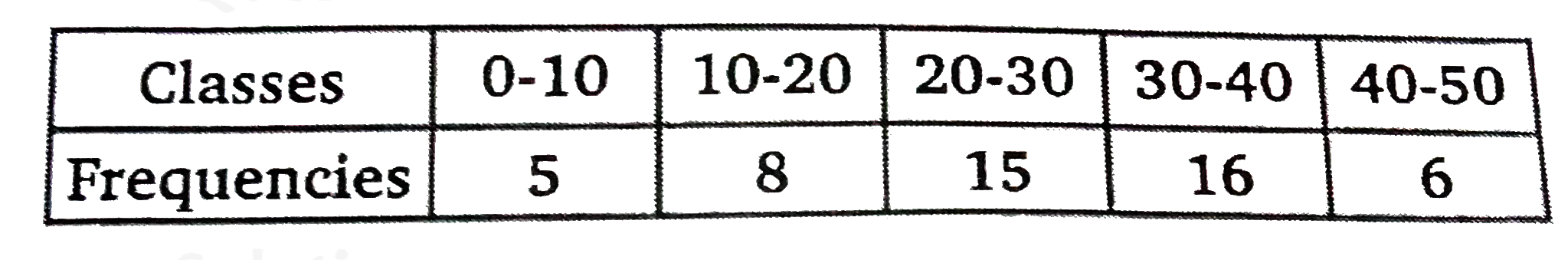 View Solution
View SolutionFind the mean and variance for the following frequency distributions in
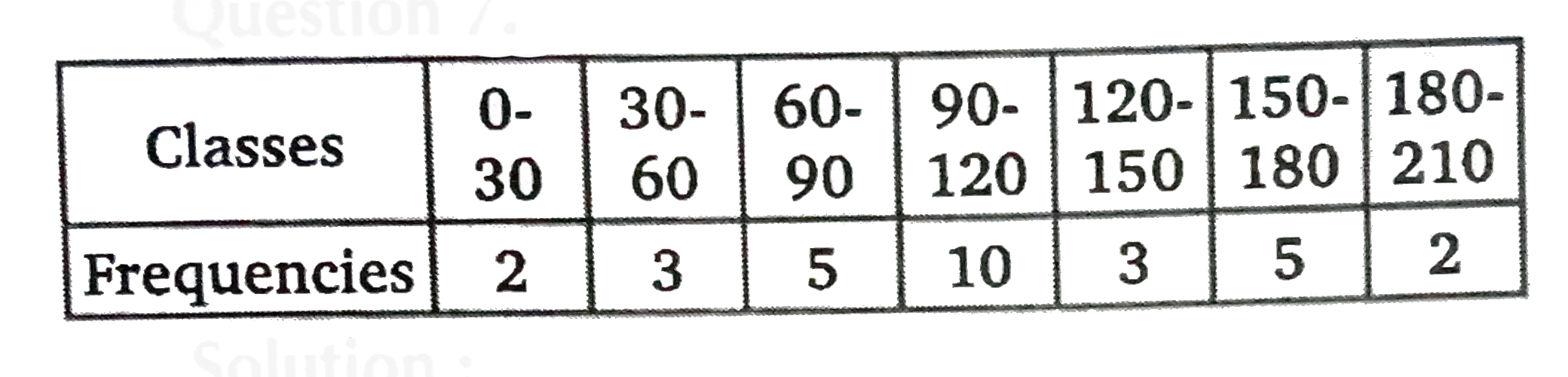 View Solution
View SolutionFind the mean for the following frequency distribution :
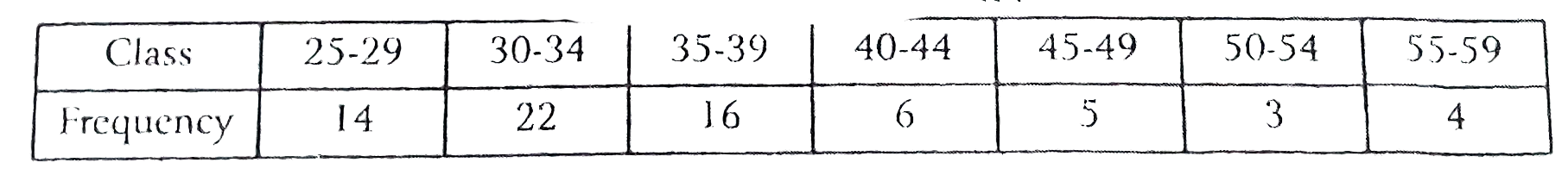 View Solution
View SolutionFind the mean and variance of Binomial Distribution if p=1/2 ,n=1
View SolutionCompute the variance of X whose distribution is given by
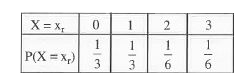 View Solution
View SolutionFind the mean and variance of the random variable X whose distribution is
 View Solution
View SolutionFind the mean of the following frequency distribution by direct method.
 View Solution
View SolutionFind the mean and standard deviation of the following frequency distribution :
 View Solution
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016View SolutionFind the mean and variance for the following probability distribution: ∣∣∣xi1234pi0.40.30.20.1∣∣∣
View Solution

