Find the mean deviation about the median for the data given below.
To find the mean deviation about the median for the given data set, we will follow these steps:
Step 1: Arrange the data in ascending order
The given data is:
45,36,50,60,53,46,51,48,72,42.
Arranging this data in ascending order gives us:
36,42,45,46,48,50,51,53,60,72.
Step 2: Find the median
Since there are 10 observations (n = 10), the median is calculated using the formula:
\(
\text{Median} = \frac{\text{n/2 th term} + \text{(n/2 + 1) th term}}{2}
\)
Here, n/2 = 5, so we need to find the 5th and 6th terms.
The 5th term is 48 and the 6th term is 50. Therefore:
\(
\text{Median} = \frac{48 + 50}{2} = \frac{98}{2} = 49.
\)
Step 3: Calculate the deviations from the median
Now we will calculate the absolute deviations of each observation from the median (49):
- |36 - 49| = 13
- |42 - 49| = 7
- |45 - 49| = 4
- |46 - 49| = 3
- |48 - 49| = 1
- |50 - 49| = 1
- |51 - 49| = 2
- |53 - 49| = 4
- |60 - 49| = 11
- |72 - 49| = 23
Step 4: Sum the absolute deviations
Now, we sum all the absolute deviations:
\(
13 + 7 + 4 + 3 + 1 + 1 + 2 + 4 + 11 + 23 = 69.
\)
Step 5: Calculate the mean deviation
Finally, we calculate the mean deviation by dividing the total absolute deviation by the number of observations:
\(
\text{Mean Deviation} = \frac{\text{Total Absolute Deviation}}{\text{Number of Observations}} = \frac{69}{10} = 6.9.
\)
Final Answer
The mean deviation about the median for the given data is 6.9.
---
The given data is:
45,36,50,60,53,46,51,48,72,42.
36,42,45,46,48,50,51,53,60,72.
Since there are 10 observations (n = 10), the median is calculated using the formula:
\(
\text{Median} = \frac{\text{n/2 th term} + \text{(n/2 + 1) th term}}{2}
\)
Here, n/2 = 5, so we need to find the 5th and 6th terms.
\(
\text{Median} = \frac{48 + 50}{2} = \frac{98}{2} = 49.
\)
Now we will calculate the absolute deviations of each observation from the median (49):
- |36 - 49| = 13
- |42 - 49| = 7
- |45 - 49| = 4
- |46 - 49| = 3
- |48 - 49| = 1
- |50 - 49| = 1
- |51 - 49| = 2
- |53 - 49| = 4
- |60 - 49| = 11
- |72 - 49| = 23
Now, we sum all the absolute deviations:
\(
13 + 7 + 4 + 3 + 1 + 1 + 2 + 4 + 11 + 23 = 69.
\)
Finally, we calculate the mean deviation by dividing the total absolute deviation by the number of observations:
\(
\text{Mean Deviation} = \frac{\text{Total Absolute Deviation}}{\text{Number of Observations}} = \frac{69}{10} = 6.9.
\)
The mean deviation about the median for the given data is 6.9.
Topper's Solved these Questions
- STATISTICSBOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - Miscellaneous word problems (EXAMPLE)
6 Videos
- STATISTICSBOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30A
18 Videos
- SOME SPECIAL SERIESBOOK - RS AGGARWALCHAPTER - SOME SPECIAL SERIESEXERCISE - EXERCISE 13B (Very short Answer Questions)
9 Videos
- STRAIGHT LINES BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE 20K
10 Videos
Similar Questions
Knowledge Check
Find the mean deviation about the median for the data given below :
11, 3, 8, 7, 5, 14, 10, 2, 9A4B5C3D6
Find the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the data is Question:

View SolutionFind the mean deviation about the mean for the data is Question:

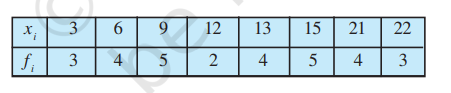
View SolutionFind the mean deviation about the median for the following data:
View SolutionFind the mean deviation about the mean for the following data :
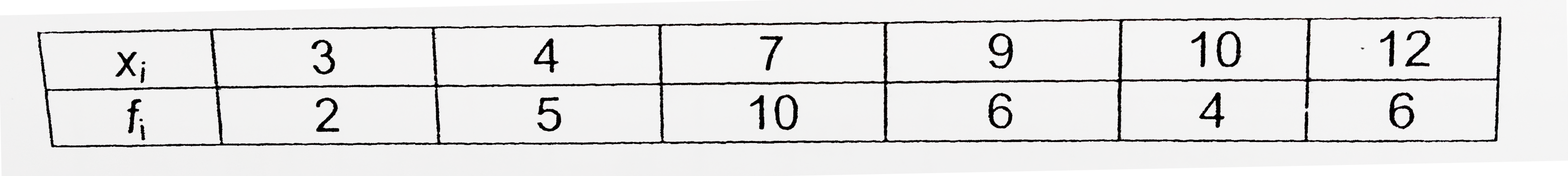
View SolutionFind the mean deviation about the mean for the following data :

View Solution