Find the mean deviation about the median for the following data:3,9,5,3,12,10,18,4,7,19,21.
To find the mean deviation about the median for the given data set 3,9,5,3,12,10,18,4,7,19,21, we will follow these steps:
Step 1: Arrange the data in ascending order
First, we need to arrange the data in ascending order:
3,3,4,5,7,9,10,12,18,19,21
Step 2: Find the median
The number of observations n is 11 (which is odd). The median is given by the formula:
Median=the (n+12)th term
Calculating:
11+12=122=6
The 6th term in the ordered data is 9. Therefore, the median m is:
m=9
Step 3: Calculate the absolute deviations from the median
Next, we calculate the absolute deviations of each data point from the median:
|x−m|=|x−9|
Calculating each deviation:
- For 3: |3−9|=6
- For 3: |3−9|=6
- For 4: |4−9|=5
- For 5: |5−9|=4
- For 7: |7−9|=2
- For 9: |9−9|=0
- For 10: |10−9|=1
- For 12: |12−9|=3
- For 18: |18−9|=9
- For 19: |19−9|=10
- For 21: |21−9|=12
Step 4: Sum the absolute deviations
Now, we sum all the absolute deviations:
6+6+5+4+2+0+1+3+9+10+12=58
Step 5: Calculate the mean deviation
The mean deviation is calculated by dividing the sum of absolute deviations by the total number of observations:
Mean Deviation=Σ|x−m|n=5811≈5.27
Final Answer
Thus, the mean deviation about the median is approximately:
Mean Deviation≈5.27
---
First, we need to arrange the data in ascending order:
3,3,4,5,7,9,10,12,18,19,21
The number of observations n is 11 (which is odd). The median is given by the formula:
Median=the (n+12)th term
Calculating:
11+12=122=6
The 6th term in the ordered data is 9. Therefore, the median m is:
m=9
Next, we calculate the absolute deviations of each data point from the median:
|x−m|=|x−9|
Calculating each deviation:
- For 3: |3−9|=6
- For 3: |3−9|=6
- For 4: |4−9|=5
- For 5: |5−9|=4
- For 7: |7−9|=2
- For 9: |9−9|=0
- For 10: |10−9|=1
- For 12: |12−9|=3
- For 18: |18−9|=9
- For 19: |19−9|=10
- For 21: |21−9|=12
Now, we sum all the absolute deviations:
6+6+5+4+2+0+1+3+9+10+12=58
The mean deviation is calculated by dividing the sum of absolute deviations by the total number of observations:
Mean Deviation=Σ|x−m|n=5811≈5.27
Thus, the mean deviation about the median is approximately:
Mean Deviation≈5.27
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 15.35videos
STATISTICS
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 15.112videos
STATISTICS
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERT ENGLISHCHAPTER - SETSEXERCISE - EXERCISE 1.57videos
SETS
- BOOK - NCERT ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.44videos
STRAIGHT LINES
Similar Questions
Find the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the mean for the following data.
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation from the median for the following data:
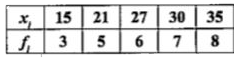 View Solution
View SolutionFind the mean deviation about median for the following data:
 View Solution
View SolutionFind the mean deviation about the median for the following data:4,6,9,3,10,13,2
View SolutionFind the mean deviation about mean for the following data:
 View Solution
View SolutionFind the mean deviation about the median for the following data:
11, 3, 8, 7, 5, 14, 10, 2, 9View SolutionFind the mean deviation about the mean for the following data:6,7,10,12,13,4,8,12
View Solution
