Find the mean deviation from the mean of the following data:
Classes:, 10-20,
20-30, 30-40, 40-50, 50-60, 60-70, 70-80
freequency:2,
3, 8, 14, 8, 3, 2
To find the mean deviation from the mean for the given data, we will follow these steps:
Step 1: Create a frequency distribution table
We will create a table with the classes, mid-values (x_i), frequencies (f_i), and the product of frequency and mid-values (f_i * x_i).
| Class | Mid-value (x_i) | Frequency (f_i) | f_i * x_i |
|----------|------------------|-----------------|-----------|
| 10-20 | 15 | 2 | 30 |
| 20-30 | 25 | 3 | 75 |
| 30-40 | 35 | 8 | 280 |
| 40-50 | 45 | 14 | 630 |
| 50-60 | 55 | 8 | 440 |
| 60-70 | 65 | 3 | 195 |
| 70-80 | 75 | 2 | 150 |
| Total| | 40 | 1800 |
Step 2: Calculate the mean (x̄)
To find the mean, we use the formula:
¯x=Σ(fi⋅xi)Σfi
Substituting the values:
¯x=180040=45
Step 3: Calculate the deviations from the mean (D_i)
Now we will calculate the deviations from the mean for each mid-value (x_i):
Di=|xi−¯x|
| Class | Mid-value (x_i) | D_i |
|----------|------------------|-------|
| 10-20 | 15 | 30 |
| 20-30 | 25 | 20 |
| 30-40 | 35 | 10 |
| 40-50 | 45 | 0 |
| 50-60 | 55 | 10 |
| 60-70 | 65 | 20 |
| 70-80 | 75 | 30 |
Step 4: Calculate f_i * |D_i|
Next, we will calculate the product of frequency and the absolute deviation:
| Class | Frequency (f_i) | D_i | f_i * |D_i| |
|----------|-----------------|-------|-------|
| 10-20 | 2 | 30 | 60 |
| 20-30 | 3 | 20 | 60 |
| 30-40 | 8 | 10 | 80 |
| 40-50 | 14 | 0 | 0 |
| 50-60 | 8 | 10 | 80 |
| 60-70 | 3 | 20 | 60 |
| 70-80 | 2 | 30 | 60 |
| Total| | | 400|
Step 5: Calculate the mean deviation (MD)
Finally, we calculate the mean deviation using the formula:
MD=Σ(fi⋅|Di|)Σfi
Substituting the values:
MD=40040=10
Final Result
The mean deviation from the mean of the given data is 10.
---
We will create a table with the classes, mid-values (x_i), frequencies (f_i), and the product of frequency and mid-values (f_i * x_i).
|----------|------------------|-----------------|-----------|
| 10-20 | 15 | 2 | 30 |
| 20-30 | 25 | 3 | 75 |
| 30-40 | 35 | 8 | 280 |
| 40-50 | 45 | 14 | 630 |
| 50-60 | 55 | 8 | 440 |
| 60-70 | 65 | 3 | 195 |
| 70-80 | 75 | 2 | 150 |
| Total| | 40 | 1800 |
To find the mean, we use the formula:
Now we will calculate the deviations from the mean for each mid-value (x_i):
|----------|------------------|-------|
| 10-20 | 15 | 30 |
| 20-30 | 25 | 20 |
| 30-40 | 35 | 10 |
| 40-50 | 45 | 0 |
| 50-60 | 55 | 10 |
| 60-70 | 65 | 20 |
| 70-80 | 75 | 30 |
Next, we will calculate the product of frequency and the absolute deviation:
|----------|-----------------|-------|-------|
| 10-20 | 2 | 30 | 60 |
| 20-30 | 3 | 20 | 60 |
| 30-40 | 8 | 10 | 80 |
| 40-50 | 14 | 0 | 0 |
| 50-60 | 8 | 10 | 80 |
| 60-70 | 3 | 20 | 60 |
| 70-80 | 2 | 30 | 60 |
| Total| | | 400|
Finally, we calculate the mean deviation using the formula:
The mean deviation from the mean of the given data is 10.
Similar Questions
Find the mean deviation from the mean of the following data:
Classes:, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
freequency:2, 3, 8, 14, 8, 3, 2
View SolutionFind the about the mean for the following data:
Marks obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
Number of students, 2, 3, 8, 14, 8, 3, 2
View SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View SolutionCalculate the median deviation from the median of the following data: Wages per week (in Rs.), 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 No. of workers, 4, 6, 10, 20, 10, 6, 4
View SolutionFind the mean deviation about median for the following data
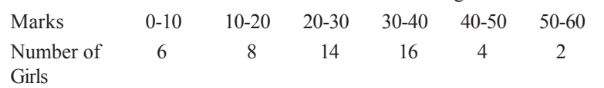
View SolutionFind out the arithmetic mean by the Step-deviation Method of the following:
Class Interval0−1010−2020−3030−4040−5050−6060−7070−80Frequency 12 16 32 52 42 32 18 12
View SolutionFind out the arithmetic mean by the Step-deviation Method of the following:
Class Interval0−1010−2020−3030−4040−5050−6060−7070−80Frequency 12 16 32 52 42 32 18 12
View SolutionFind the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547
View SolutionUsing step deviation method find the standard deviation and its coeficient of the following data.Class 20−30,40−50,50−60,60−70,70−80,80−90 and Frequency 3,61,132,153,140,51,2
View SolutionFind the median of the following data: class : 0−10,equency:5, 10−20,3, 20−30,4, 30−40,3, 40−50,3,50-60 , 4,60-70 , 7, 70-80 , 9,80-90 , 7,90-100 , 8,
View Solution
