Find the mean marks of the students from the following cumulative frequency distribution: Marks: Below Below Below Below Below Below Below Below Below Below 10 20 30 40 50 60 70 80 90 100 No. of Students 5 9 17 29 45 60 70 78 83 85
To find the mean marks of the students from the given cumulative frequency distribution, we will follow these steps:
Step 1: Create a Frequency Table
We need to convert the cumulative frequency data into a frequency distribution. The cumulative frequency tells us how many students scored below a certain mark. To find the frequency for each class interval, we subtract the cumulative frequency of the previous interval from the current one.
| Marks Interval | Cumulative Frequency | Frequency (f) |
|----------------|----------------------|----------------|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 9 | 9 - 5 = 4 |
| 20 - 30 | 17 | 17 - 9 = 8 |
| 30 - 40 | 29 | 29 - 17 = 12 |
| 40 - 50 | 45 | 45 - 29 = 16 |
| 50 - 60 | 60 | 60 - 45 = 15 |
| 60 - 70 | 70 | 70 - 60 = 10 |
| 70 - 80 | 78 | 78 - 70 = 8 |
| 80 - 90 | 83 | 83 - 78 = 5 |
| 90 - 100 | 85 | 85 - 83 = 2 |
So, the frequency table is:
| Marks Interval | Frequency (f) |
|----------------|----------------|
| 0 - 10 | 5 |
| 10 - 20 | 4 |
| 20 - 30 | 8 |
| 30 - 40 | 12 |
| 40 - 50 | 16 |
| 50 - 60 | 15 |
| 60 - 70 | 10 |
| 70 - 80 | 8 |
| 80 - 90 | 5 |
| 90 - 100 | 2 |
Step 2: Calculate Mid Values (X)
Next, we calculate the mid-value (X) for each class interval. The mid-value is calculated as follows:
X=Lower limit+Upper limit2
| Marks Interval | Mid Value (X) |
|----------------|----------------|
| 0 - 10 | 5 |
| 10 - 20 | 15 |
| 20 - 30 | 25 |
| 30 - 40 | 35 |
| 40 - 50 | 45 |
| 50 - 60 | 55 |
| 60 - 70 | 65 |
| 70 - 80 | 75 |
| 80 - 90 | 85 |
| 90 - 100 | 95 |
Step 3: Calculate f * X
Now, we multiply the frequency (f) by the mid-value (X) for each class interval.
| Marks Interval | Frequency (f) | Mid Value (X) | f * X |
|----------------|----------------|----------------|---------|
| 0 - 10 | 5 | 5 | 25 |
| 10 - 20 | 4 | 15 | 60 |
| 20 - 30 | 8 | 25 | 200 |
| 30 - 40 | 12 | 35 | 420 |
| 40 - 50 | 16 | 45 | 720 |
| 50 - 60 | 15 | 55 | 825 |
| 60 - 70 | 10 | 65 | 650 |
| 70 - 80 | 8 | 75 | 600 |
| 80 - 90 | 5 | 85 | 425 |
| 90 - 100 | 2 | 95 | 190 |
Step 4: Calculate Total Frequency and Total of f * X
Now, we sum the frequency and the f * X values.
- Total Frequency (Σf) = 5 + 4 + 8 + 12 + 16 + 15 + 10 + 8 + 5 + 2 = 85
- Total of f * X (Σf * X) = 25 + 60 + 200 + 420 + 720 + 825 + 650 + 600 + 425 + 190 = 3095
Step 5: Calculate the Mean
Finally, we can calculate the mean using the formula:
Mean=Σf⋅XΣf=309585≈36.41
Final Answer
The mean marks of the students is approximately 36.41.
We need to convert the cumulative frequency data into a frequency distribution. The cumulative frequency tells us how many students scored below a certain mark. To find the frequency for each class interval, we subtract the cumulative frequency of the previous interval from the current one.
|----------------|----------------------|----------------|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 9 | 9 - 5 = 4 |
| 20 - 30 | 17 | 17 - 9 = 8 |
| 30 - 40 | 29 | 29 - 17 = 12 |
| 40 - 50 | 45 | 45 - 29 = 16 |
| 50 - 60 | 60 | 60 - 45 = 15 |
| 60 - 70 | 70 | 70 - 60 = 10 |
| 70 - 80 | 78 | 78 - 70 = 8 |
| 80 - 90 | 83 | 83 - 78 = 5 |
| 90 - 100 | 85 | 85 - 83 = 2 |
|----------------|----------------|
| 0 - 10 | 5 |
| 10 - 20 | 4 |
| 20 - 30 | 8 |
| 30 - 40 | 12 |
| 40 - 50 | 16 |
| 50 - 60 | 15 |
| 60 - 70 | 10 |
| 70 - 80 | 8 |
| 80 - 90 | 5 |
| 90 - 100 | 2 |
Next, we calculate the mid-value (X) for each class interval. The mid-value is calculated as follows:
|----------------|----------------|
| 0 - 10 | 5 |
| 10 - 20 | 15 |
| 20 - 30 | 25 |
| 30 - 40 | 35 |
| 40 - 50 | 45 |
| 50 - 60 | 55 |
| 60 - 70 | 65 |
| 70 - 80 | 75 |
| 80 - 90 | 85 |
| 90 - 100 | 95 |
Now, we multiply the frequency (f) by the mid-value (X) for each class interval.
|----------------|----------------|----------------|---------|
| 0 - 10 | 5 | 5 | 25 |
| 10 - 20 | 4 | 15 | 60 |
| 20 - 30 | 8 | 25 | 200 |
| 30 - 40 | 12 | 35 | 420 |
| 40 - 50 | 16 | 45 | 720 |
| 50 - 60 | 15 | 55 | 825 |
| 60 - 70 | 10 | 65 | 650 |
| 70 - 80 | 8 | 75 | 600 |
| 80 - 90 | 5 | 85 | 425 |
| 90 - 100 | 2 | 95 | 190 |
Now, we sum the frequency and the f * X values.
- Total of f * X (Σf * X) = 25 + 60 + 200 + 420 + 720 + 825 + 650 + 600 + 425 + 190 = 3095
Finally, we can calculate the mean using the formula:
The mean marks of the students is approximately 36.41.
Topper's Solved these Questions
Similar Questions
Find the area of the figure given below.
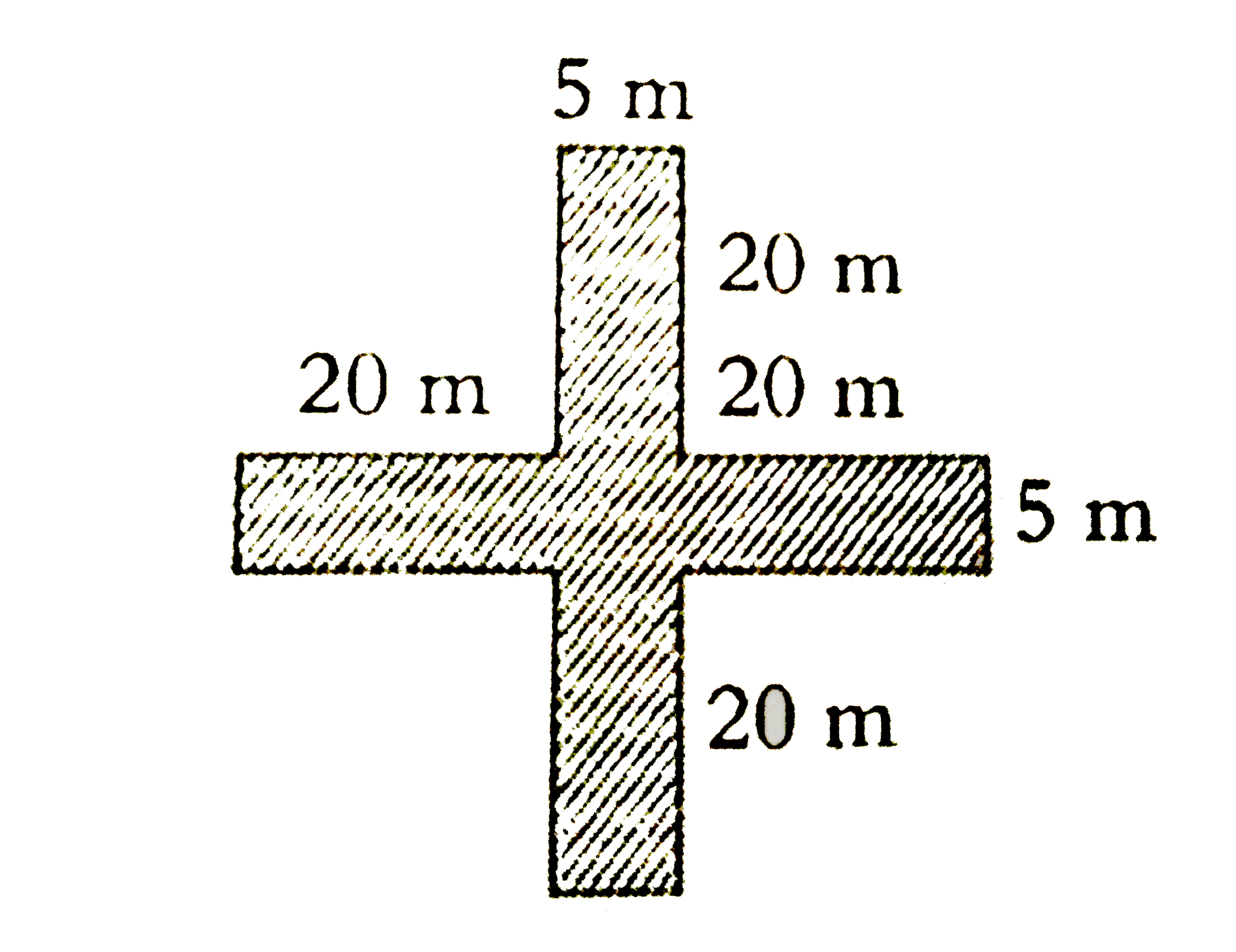 View Solution
View SolutionFor the system given below, find the angular frequency of oscillation?
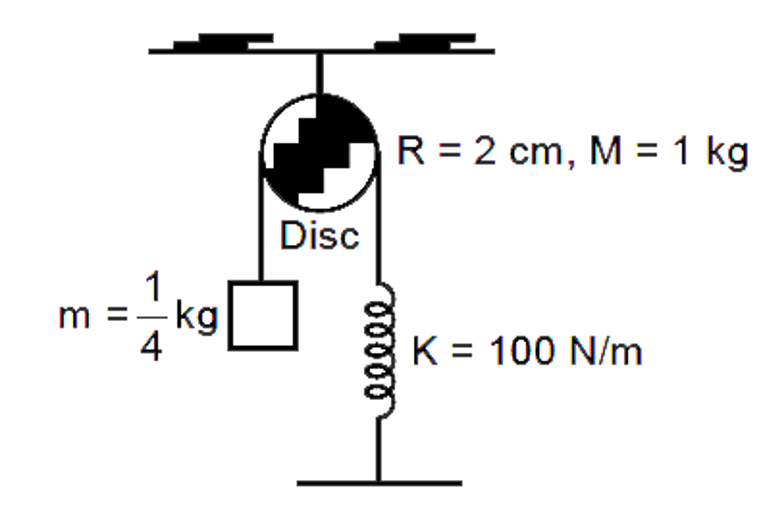 View Solution
View SolutionFind the frequency of the waves given below.
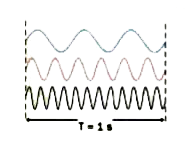 View Solution
View SolutionA cumulative frequency distribution is given below. Convert this into a frequency distribution table. Marks Below 45 Below 60 Below 75 Below 90 Below 105 Below 120 No. of Students 0 8 23 48 85 116
View SolutionA cumulative frequency distribution is given below. Convert this into a frequency distribution table. Marks Below 45 Below 60 Below 75 Below 90 Below 105 Below 120 No. of Students 0 8 23 48 85 116
View SolutionGiven below are the cumulative frequencies showing the weights of 685 students of a school. Prepare a frequency distribution table. Weight (in kg), No. of students Below 25 Below 30 Below 35 Below 40 Below 45 Below 50 Below 55 Below 60 Below 65 Below 70, 0 24 78 183 294 408 543 621 674 685
View SolutionWhich of the statements below is correct?
View SolutionFind the mean of the frequency distribution:
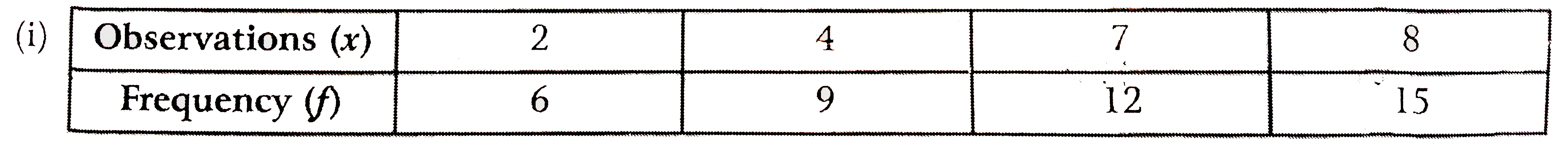
(ii) The weight of 40 students of class IX are given below:
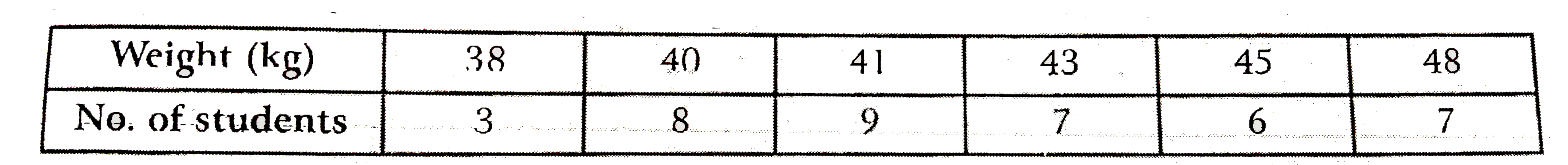 View Solution
View SolutionIdentify the polymer given below
 View Solution
View SolutionName the sounds of the frequencies given below:
40 HzView Solution

