Find the mean, variance and standard deviation of the number heads when three coins are tossed.
To find the mean, variance, and standard deviation of the number of heads when three coins are tossed, we can follow these steps:
Step 1: Identify the Sample Space
When three coins are tossed, the possible outcomes can be represented as:
- HHH (3 heads)
- HHT (2 heads)
- HTH (2 heads)
- THH (2 heads)
- HTT (1 head)
- THT (1 head)
- TTH (1 head)
- TTT (0 heads)
Thus, the sample space S is:
S={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
Step 2: Count the Number of Heads
Next, we count the number of heads for each outcome:
- 3 heads: HHH (1 way)
- 2 heads: HHT, HTH, THH (3 ways)
- 1 head: HTT, THT, TTH (3 ways)
- 0 heads: TTT (1 way)
Step 3: Create a Probability Distribution
Now, we can create a probability distribution for the number of heads:
- X=0: Probability P(X=0)=18
- X=1: Probability P(X=1)=38
- X=2: Probability P(X=2)=38
- X=3: Probability P(X=3)=18
Step 4: Calculate the Mean
The mean μ is calculated using the formula:
μ=E(X)=∑(xi⋅P(X=xi))
Calculating:
μ=(0⋅18)+(1⋅38)+(2⋅38)+(3⋅18)
=0+38+68+38
=128=1.5
Step 5: Calculate the Variance
The variance σ2 is calculated using the formula:
σ2=E(X2)−(E(X))2
First, calculate E(X2):
E(X2)=∑(x2i⋅P(X=xi))
Calculating:
E(X2)=(02⋅18)+(12⋅38)+(22⋅38)+(32⋅18)
=0+38+128+98
=248=3
Now, substituting into the variance formula:
σ2=3−(1.5)2=3−2.25=0.75
Step 6: Calculate the Standard Deviation
The standard deviation σ is the square root of the variance:
σ=√σ2=√0.75≈0.866
Final Results
- Mean μ=1.5
- Variance σ2=0.75
- Standard Deviation σ≈0.866
When three coins are tossed, the possible outcomes can be represented as:
- HHH (3 heads)
- HHT (2 heads)
- HTH (2 heads)
- THH (2 heads)
- HTT (1 head)
- THT (1 head)
- TTH (1 head)
- TTT (0 heads)
S={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
Next, we count the number of heads for each outcome:
- 3 heads: HHH (1 way)
- 2 heads: HHT, HTH, THH (3 ways)
- 1 head: HTT, THT, TTH (3 ways)
- 0 heads: TTT (1 way)
Now, we can create a probability distribution for the number of heads:
- X=0: Probability P(X=0)=18
- X=1: Probability P(X=1)=38
- X=2: Probability P(X=2)=38
- X=3: Probability P(X=3)=18
The mean μ is calculated using the formula:
μ=E(X)=∑(xi⋅P(X=xi))
μ=(0⋅18)+(1⋅38)+(2⋅38)+(3⋅18)
=0+38+68+38
=128=1.5
The variance σ2 is calculated using the formula:
σ2=E(X2)−(E(X))2
E(X2)=∑(x2i⋅P(X=xi))
Calculating:
E(X2)=(02⋅18)+(12⋅38)+(22⋅38)+(32⋅18)
=0+38+128+98
=248=3
σ2=3−(1.5)2=3−2.25=0.75
The standard deviation σ is the square root of the variance:
σ=√σ2=√0.75≈0.866
- Mean μ=1.5
- Variance σ2=0.75
- Standard Deviation σ≈0.866
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 3118videos
PROBABILITY DISTRIBUTION
- BOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Objective Questions30videos
PROBABILITY DISTRIBUTION
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B2videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions34videos
PRODUCT OF THREE VECTORS
Similar Questions
Determine variance and standard deviation of the number of heads in three tosses of a coin.
View SolutionFind the mean, variance and standard deviation of the number of tails in two tosses of a coin.
View SolutionFind the mean, variance and standard deviation of first n natural numbers.
View SolutionFind the mean variance and standard deviation using short-cut method
 View Solution
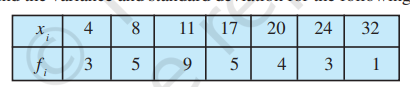
View SolutionFind the mean, variance and standard deviation using short-cut method
 View Solution
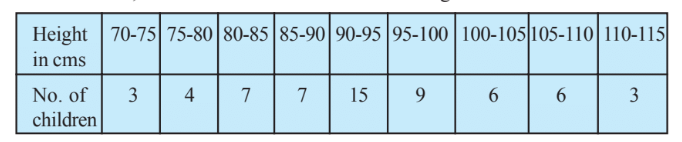
View SolutionFind the variance and standard deviation for the following data:
 View Solution
View SolutionFind the mean, variance and standard deviation using short-cut method.
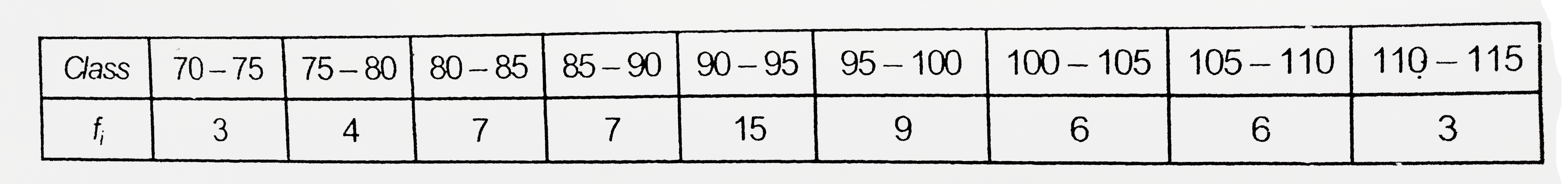 View Solution
View SolutionFind the mean, variance, standard deviation of number 6 in the two throws of a dice.
View SolutionFind the probability distribution of the number of heads when three coins are tossed.
View Solution(a) (i) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
(ii) Find the probability distribution of the number of tails in the simultaneous tosses of three coins.
(iii) Find the probability distribution of the number of heads in the simultaneous toss of four coins.
(b) (i) Find the probability distribution of the number of heads in three tosses of a coin.
(ii) Find the probability distribution of the number of sixes in two tosses of a die.
( c ) Find the probability distribution of the number of heads (tails) in four tosses of a coin.View Solution

