In the items produced by a factory there are 10% defective items A sample of 6 items is randomly chosen . Find the probability that this sample contains (i) exactly 2 defective items (ii) not more than 2 defective items (iii) at least 3 defective items .
The correct Answer is:(i).320×(910)4(ii).32×(1920)4(iii)1−[32×(1920)4]
To solve the problem, we need to use the binomial probability formula, which is given by:
P(X=r)=(nr)prqn−r
where:
- n is the total number of trials (in this case, the number of items sampled),
- r is the number of successful trials (defective items),
- p is the probability of success (probability of an item being defective),
- q is the probability of failure (probability of an item being non-defective).
Given:
- The probability of a defective item p=0.1 (10% defective),
- The probability of a non-defective item q=1−p=0.9,
- The sample size n=6.
Step 1: Calculate the probability of exactly 2 defective items
We need to find P(X=2):
P(X=2)=(62)(0.1)2(0.9)6−2
Calculating (62):
(62)=6!2!(6−2)!=6×52×1=15
Now substituting back into the formula:
P(X=2)=15×(0.1)2×(0.9)4
Calculating (0.1)2=0.01 and (0.9)4=0.6561:
P(X=2)=15×0.01×0.6561=15×0.006561=0.098415
Thus, the probability of exactly 2 defective items is approximately 0.0984.
Step 2: Calculate the probability of not more than 2 defective items
We need to find P(X≤2):
P(X≤2)=P(X=0)+P(X=1)+P(X=2)
Calculating P(X=0):
P(X=0)=(60)(0.1)0(0.9)6=1×1×0.531441=0.531441
Calculating P(X=1):
P(X=1)=(61)(0.1)1(0.9)5=6×0.1×0.59049=6×0.059049=0.354294
Now, we can sum these probabilities:
P(X≤2)=P(X=0)+P(X=1)+P(X=2)
P(X≤2)=0.531441+0.354294+0.098415=0.98415
Thus, the probability of not more than 2 defective items is approximately 0.9842.
Step 3: Calculate the probability of at least 3 defective items
We need to find P(X≥3):
P(X≥3)=1−P(X<3)=1−P(X≤2)
From Step 2, we already calculated P(X≤2):
P(X≥3)=1−0.98415=0.01585
Thus, the probability of at least 3 defective items is approximately 0.0159.
Summary of Results:
1. Probability of exactly 2 defective items: 0.0984
2. Probability of not more than 2 defective items: 0.9842
3. Probability of at least 3 defective items: 0.0159
- n is the total number of trials (in this case, the number of items sampled),
- r is the number of successful trials (defective items),
- p is the probability of success (probability of an item being defective),
- q is the probability of failure (probability of an item being non-defective).
- The probability of a defective item p=0.1 (10% defective),
- The probability of a non-defective item q=1−p=0.9,
- The sample size n=6.
P(X≤2)=0.531441+0.354294+0.098415=0.98415
1. Probability of exactly 2 defective items: 0.0984
2. Probability of not more than 2 defective items: 0.9842
3. Probability of at least 3 defective items: 0.0159
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBook:RS AGGARWALChapter:PROBABILITY DISTRIBUTIONExercise:Objective Questions
Explore 30 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Exercise 29 B
Explore 2 Videos
- PRODUCT OF THREE VECTORSBook:RS AGGARWALChapter:PRODUCT OF THREE VECTORSExercise:Objective Questions
Explore 34 Videos
Similar Questions
There are 10 defective bulbs in a group of 100 bulbs. If a sample of 8 bulbs are selected at random then find the probability that:
(i) in this sample 3 bulbs are defective and 5 are non-defective.
(ii) in this sample at least one bulb is defective.
View SolutionThere are 6% defective items in a large bulk of item. Find the probability that sample of 8 items will include not more than one defective items.
View Solution
Knowledge Check
Iterms produced by a compary are supposed to contain 5% defective items .probability that a sample of 8 items will contain less than 2 defective items is
A2720(1920)7B541400(1920)6C15320(120)7D3516(120)6The items produced by a firm are supposed to contain 5% defective items. The probability that a smaple of 8 items will contain will less than 2 defective items, is
A2720(1920)7B533400(1920)6C15320(120)7D3516(120)6
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?
View SolutionThere are 4 defective items in a lot consisting of 10 items. From this lot we select 5 items at random. The probability that there will be 2 defective items among them is
View SolutionThree items from a lot of 10 items are defective. if two items are selected randomly one by one without replacing then the probability that both are defective items.
View SolutionA box contains 10 bulbs, of which just three are defective. If a random sample of five bulbs is drawn , find the probabilities that the sample contains: Exactly on defective bulb. Exactly two defective bulbs. No defective bulbs.
View SolutionIf 2% of pipes manufactured by a company are defective, the probability that in a sample of 1000 pipes exactly 6 pipes are defective is
View SolutionOver the past 200 working days , the number of defective parts produced by a machine is given in the following table :
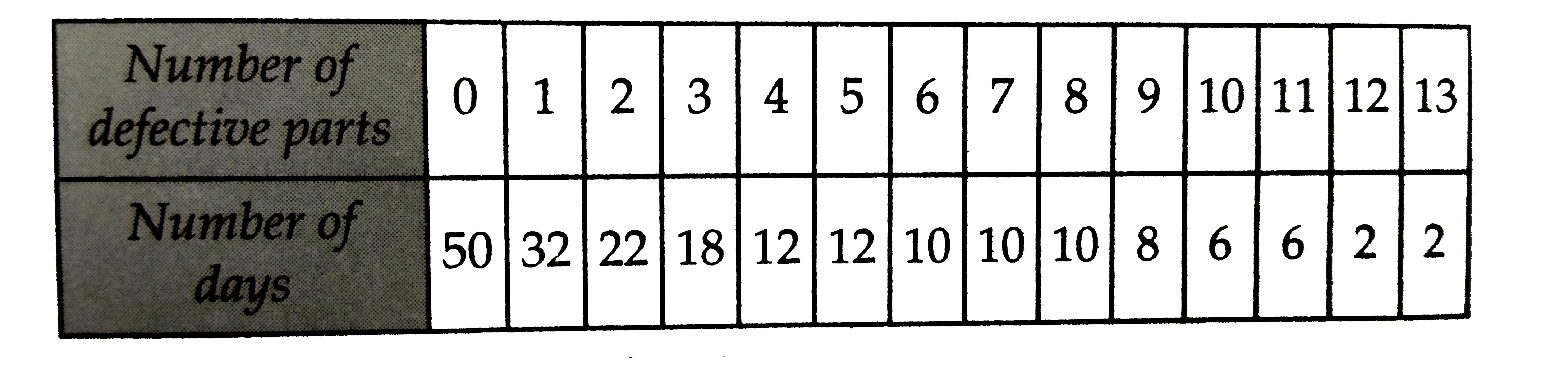
From these days , one day is chosen at random . What is the probability that on that day , the output has
(i) no defective part ?
(ii) at least 1 defective part ?
(iii) not more than 5 defective parts ?
(iv) more than 5 , but less than 8 defective parts ?
(v) more than 13 defective parts ?
View Solution