Find the median of the following data: 41, 43, 127, 99, 61, 92, 71, 58, 57. If 58 is replaced by 85, what will be the new median.
The correct Answer is:71
To find the median of the given data set and then determine the new median after replacing a number, we will follow these steps:
Step 1: Arrange the Data in Ascending Order
The original data set is:
41, 43, 127, 99, 61, 92, 71, 58, 57.
First, we will arrange this data in ascending order:
- The sorted data is: 41, 43, 57, 58, 61, 71, 92, 99, 127.
Step 2: Find the Median
The median is the middle value of a data set. Since there are 9 numbers (which is odd), the median will be the value at the position given by (n + 1) / 2, where n is the number of data points.
- Here, n = 9.
- The position of the median is (9 + 1) / 2 = 10 / 2 = 5.
Now, we find the 5th term in the sorted list:
- The 5th term is 61.
Thus, the median of the original data set is 61.
Step 3: Replace 58 with 85
Now, we will replace 58 with 85 in the original data set. The new data set will be:
41, 43, 127, 99, 61, 92, 71, 85, 57.
Step 4: Arrange the New Data in Ascending Order
Now, we will sort the new data set:
- The sorted data is: 41, 43, 57, 61, 71, 85, 92, 99, 127.
Step 5: Find the New Median
Again, since there are still 9 numbers, we will find the median using the same formula:
- The position of the median is still (9 + 1) / 2 = 10 / 2 = 5.
Now, we find the 5th term in the new sorted list:
- The 5th term is 71.
Thus, the new median after replacing 58 with 85 is 71.
Summary
- The original median was 61.
- The new median after the replacement is 71.
The original data set is:
41, 43, 127, 99, 61, 92, 71, 58, 57.
- The sorted data is: 41, 43, 57, 58, 61, 71, 92, 99, 127.
The median is the middle value of a data set. Since there are 9 numbers (which is odd), the median will be the value at the position given by (n + 1) / 2, where n is the number of data points.
- The position of the median is (9 + 1) / 2 = 10 / 2 = 5.
- The 5th term is 61.
Now, we will replace 58 with 85 in the original data set. The new data set will be:
41, 43, 127, 99, 61, 92, 71, 85, 57.
Now, we will sort the new data set:
- The sorted data is: 41, 43, 57, 61, 71, 85, 92, 99, 127.
Again, since there are still 9 numbers, we will find the median using the same formula:
- The position of the median is still (9 + 1) / 2 = 10 / 2 = 5.
- The 5th term is 71.
- The original median was 61.
- The new median after the replacement is 71.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - NCERT SECTION (Exercise 14.1)2videos
STATISTICS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - NCERT SECTION (Exercise 14.2)15videos
STATISTICS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - Olympiad/HOTS CORNER15videos
QUADRILATERALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - OLYMPAID/ HOTS CORNER10videos
TRIANGLES
Similar Questions
Find the median for the following data :
 View Solution
View SolutionFind the median for the following data :
 View Solution
View SolutionFind the median for the following data.
 View Solution
View SolutionFind the median from the following data :
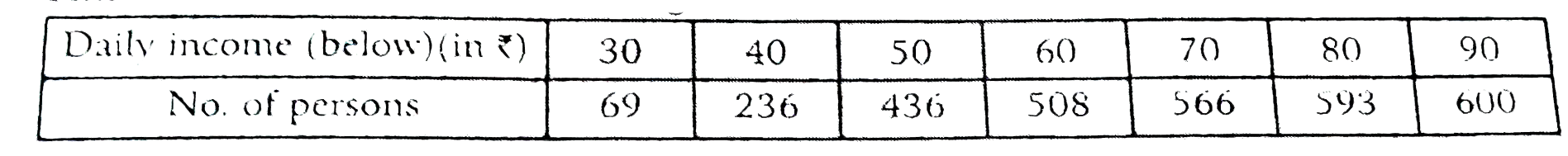 View Solution
View SolutionFind the median from the following data :
 View Solution
View SolutionFind the median from the following data :
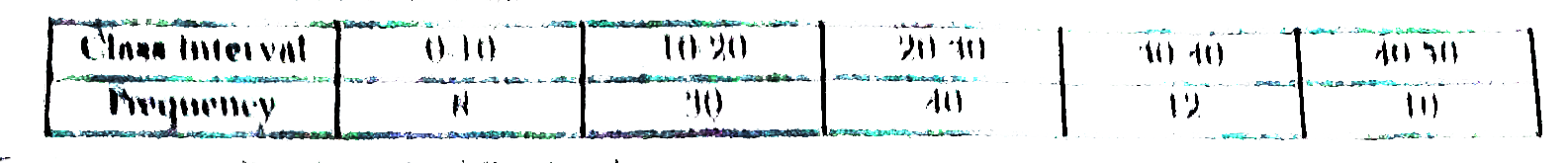 View Solution
View SolutionFind the median from the following data :
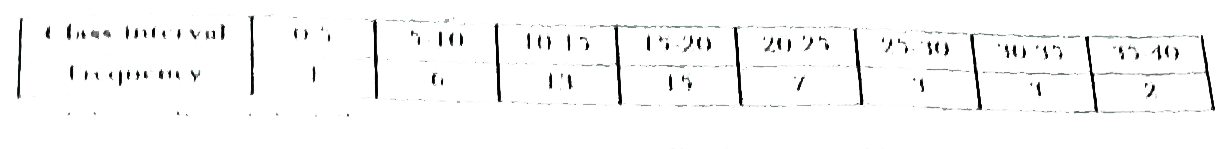 View Solution
View SolutionFind the median from the following data :
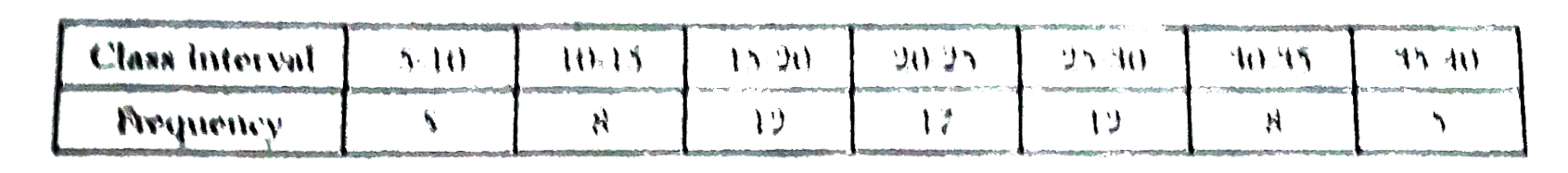 View Solution
View SolutionFind the median from the following data :
 View Solution
View SolutionFind the median from the following data :
 View Solution
View Solution

