Find the number of real solutions to the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π.
0
1
2
infinite
We have
√1+cos2x=√2sin−1(sinx)
→√2|cosx|=√2sin−1(sinx)
→|cosx|=sin−1(sinx)
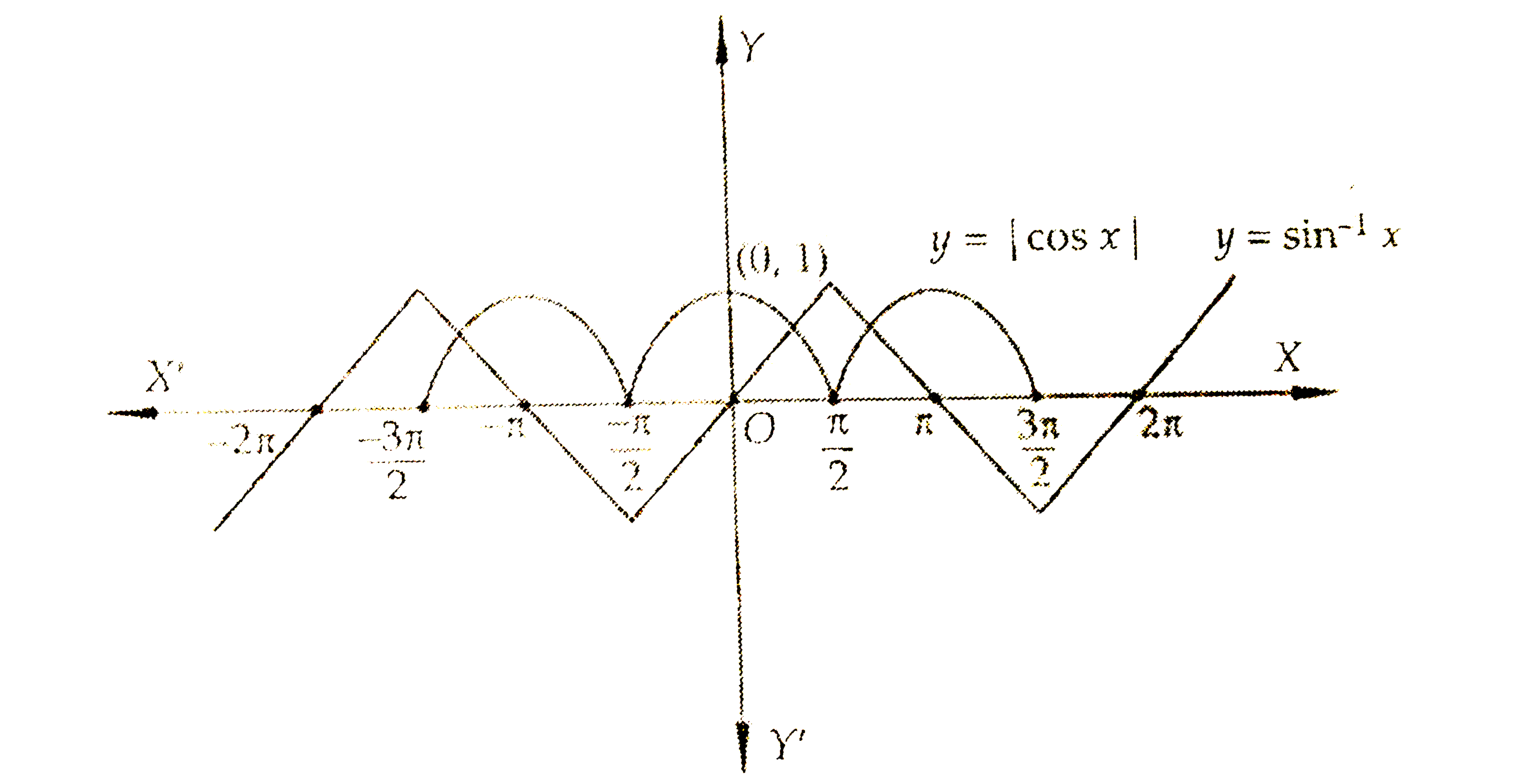
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Section II - Assertion Reason Type
Explore 11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Exercise
Explore 72 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Chapter Test
Explore 30 Videos
- INDEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INDEFINITE INTEGRALSExercise:Chapter Test
Explore 30 Videos
- LIMITSBook:OBJECTIVE RD SHARMA ENGLISHChapter:LIMITSExercise:Chapter Test
Explore 58 Videos
Similar Questions
The number of real solution of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π, is
View SolutionThe number of real solution of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π, is
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is 0 (b) 1 (c) 2 (d) infinite
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionFind the number of solutions of the equation sinx=x2+x+1.
View SolutionFind the number of solutions of the equation sinx=x2+x+1.
View SolutionFind the number of solution of the equation sinx=x2+x+1.
View SolutionThe number of real solutions of the equation
√1+cos2x=√2cos−1(cosx) in [π2,π] is
View SolutionFind the number of real solutions of the equation sin−1(ex)+cos−1(x2)=π/2.
View Solution