Find the number of rectangles excluding squares from a rectangle of size 9 × 6.
To find the number of rectangles excluding squares from a rectangle of size 9 × 6, we can follow these steps:
Step 1: Calculate the total number of rectangles
To find the total number of rectangles in a rectangle of size 9 × 6, we need to determine how many horizontal and vertical lines we can draw.
- A rectangle of size 9 × 6 has 10 horizontal lines (9 + 1) and 7 vertical lines (6 + 1).
- The number of ways to choose 2 horizontal lines from 10 is given by (102).
- The number of ways to choose 2 vertical lines from 7 is given by (72).
Thus, the total number of rectangles is:
Total Rectangles=(102)×(72)
Calculating these:
(102)=10×92×1=45
(72)=7×62×1=21
So, the total number of rectangles is:
45×21=945
Step 2: Calculate the total number of squares
Next, we need to calculate the total number of squares that can be formed within the 9 × 6 rectangle.
The number of squares of size k×k that can fit in a rectangle is given by:
(9−k+1)×(6−k+1)
for each possible size k.
We can have squares of sizes 1 to 6 (the maximum size is limited by the shorter side of the rectangle, which is 6).
Calculating the number of squares for each size:
- For k=1: 8×5=40
- For k=2: 7×4=28
- For k=3: 6×3=18
- For k=4: 5×2=10
- For k=5: 4×1=4
- For k=6: 3×0=0
Now, summing these values gives:
40+28+18+10+4+0=100
Step 3: Exclude squares from rectangles
Finally, to find the number of rectangles excluding squares, we subtract the total number of squares from the total number of rectangles:
Rectangles excluding squares=Total Rectangles−Total Squares=945−100=845
Final Answer
The number of rectangles excluding squares from a rectangle of size 9 × 6 is 845.
---
To find the total number of rectangles in a rectangle of size 9 × 6, we need to determine how many horizontal and vertical lines we can draw.
- The number of ways to choose 2 horizontal lines from 10 is given by (102).
- The number of ways to choose 2 vertical lines from 7 is given by (72).
Total Rectangles=(102)×(72)
(102)=10×92×1=45
(72)=7×62×1=21
45×21=945
Next, we need to calculate the total number of squares that can be formed within the 9 × 6 rectangle.
(9−k+1)×(6−k+1)
for each possible size k.
- For k=1: 8×5=40
- For k=2: 7×4=28
- For k=3: 6×3=18
- For k=4: 5×2=10
- For k=5: 4×1=4
- For k=6: 3×0=0
40+28+18+10+4+0=100
Finally, to find the number of rectangles excluding squares, we subtract the total number of squares from the total number of rectangles:
Rectangles excluding squares=Total Rectangles−Total Squares=945−100=845
The number of rectangles excluding squares from a rectangle of size 9 × 6 is 845.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - JEE Type Solved Examples: Single Matching Type Questions
1 Video
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 1
11 Videos
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
Similar Questions
Knowledge Check
A square and a rectangle have :
Aonly one line of symmetry eachBtwo lines of symmetry eachCfour lines of symmetry eachDan unequal number of lines of symmetry
Find the perimeter of each rectangle.
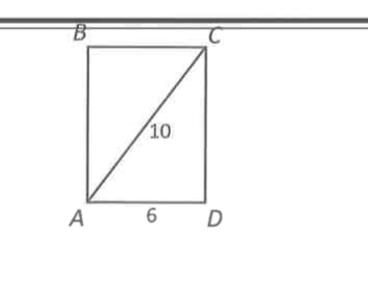
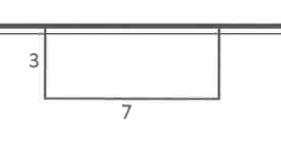
View SolutionFind the perimeter of each rectangle.
View Solution(i) Find the number of reatangles of any size in a chess board
(ii) Find the number of squares of any size in a rectangle of size 8×5 .
View SolutionFind the total number of rectangles on the normal chessboard.
View SolutionFind the total number of rectangles on the normal chessboard.
View SolutionFind number of rectangles in a chessboard, which are not a square.
View SolutionThe area of a rectangle of size 1.23×2.345cm is
View Solution