Find the total number of rectangles on the normal chessboard.
To find the total number of rectangles on a normal chessboard, we can follow these steps:
1. Understanding the Chessboard Layout:
A normal chessboard has 8 squares along each side, which means there are 9 horizontal lines and 9 vertical lines (including the edges).
2. Choosing Lines to Form Rectangles:
To form a rectangle, we need to choose 2 horizontal lines and 2 vertical lines. The intersection of these lines will give us the corners of the rectangle.
3. Calculating the Number of Ways to Choose Lines:
- The number of ways to choose 2 lines from 9 horizontal lines can be calculated using the combination formula C(n,r)=n!r!(n−r)!.
- For horizontal lines:
C(9,2)=9!2!(9−2)!=9×82×1=36
- Similarly, for vertical lines:
C(9,2)=9!2!(9−2)!=36
4. Calculating the Total Number of Rectangles:
Since the choices of horizontal and vertical lines are independent, we multiply the number of ways to choose the horizontal lines by the number of ways to choose the vertical lines:
Total Rectangles=C(9,2)×C(9,2)=36×36=1296
5. Final Answer:
The total number of rectangles on a normal chessboard is 1296.
A normal chessboard has 8 squares along each side, which means there are 9 horizontal lines and 9 vertical lines (including the edges).
To form a rectangle, we need to choose 2 horizontal lines and 2 vertical lines. The intersection of these lines will give us the corners of the rectangle.
- The number of ways to choose 2 lines from 9 horizontal lines can be calculated using the combination formula C(n,r)=n!r!(n−r)!.
- For horizontal lines:
C(9,2)=9!2!(9−2)!=9×82×1=36
C(9,2)=9!2!(9−2)!=36
Since the choices of horizontal and vertical lines are independent, we multiply the number of ways to choose the horizontal lines by the number of ways to choose the vertical lines:
Total Rectangles=C(9,2)×C(9,2)=36×36=1296
The total number of rectangles on a normal chessboard is 1296.
Topper's Solved these Questions
Similar Questions
(i) Find the number of reatangles of any size in a chess board
(ii) Find the number of squares of any size in a rectangle of size 8×5 .
View SolutionFind the perimeter of each rectangle.
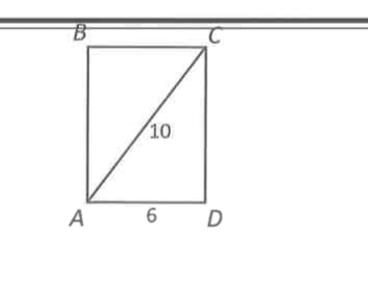
View SolutionFind the perimeter of each rectangle.
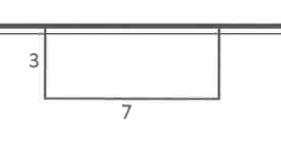
View SolutionA coin is tossed. Find the total number of elementary events and also the total number events associated with the random experiment.
View SolutionFind the total number of permutations of the letters of the word INSTITUTE.
View Solution12% of the employees in a factory are females and the number of male employees is 264. Find the total number of employees. Also, find the number of female employees.
View SolutionFind number of rectangles in a chessboard, which are not a square.
View SolutionFind the number of ways in which two small squares can be selected on the normal chessboard if they are not in same row or same column.
View SolutionFind the number of rectangles excluding squares from a rectangle of size 9 × 6.
View SolutionSee the figure and find the ratio of(a) Number of triangles to the number of circles inside the rectangle.(b) Number of squares to all the figures inside the rectangle.(c) Number of circles to all the figures inside the rectangle.
View Solution
