Find the position of point (4, 1) after it undergoes the transformations successively : Translation by one unit along x-axis in the positive direction.
To find the position of the point (4, 1) after it undergoes a transformation of translation by one unit along the x-axis in the positive direction, we can follow these steps:
Step 1: Identify the original coordinates
The original coordinates of the point are given as (4, 1).
Step 2: Understand the translation
Translation along the x-axis in the positive direction means we will increase the x-coordinate of the point by the specified amount. In this case, we are translating by 1 unit.
Step 3: Apply the translation
To apply the translation, we add 1 to the x-coordinate of the original point:
- New x-coordinate = Original x-coordinate + 1
- New x-coordinate = 4 + 1 = 5
The y-coordinate remains unchanged during this translation:
- New y-coordinate = Original y-coordinate = 1
Step 4: Write the new coordinates
After the translation, the new coordinates of the point become:
- New position = (5, 1)
Final Answer
The position of the point (4, 1) after the transformation is (5, 1).
---
The original coordinates of the point are given as (4, 1).
Translation along the x-axis in the positive direction means we will increase the x-coordinate of the point by the specified amount. In this case, we are translating by 1 unit.
To apply the translation, we add 1 to the x-coordinate of the original point:
- New x-coordinate = Original x-coordinate + 1
- New x-coordinate = 4 + 1 = 5
- New y-coordinate = Original y-coordinate = 1
After the translation, the new coordinates of the point become:
- New position = (5, 1)
The position of the point (4, 1) after the transformation is (5, 1).
Similar Questions
Find the position of point (4, 1) after it undergoes the transformations successively : Reflection about the line y=x−1
View SolutionThe point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View SolutionThe point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View SolutionThe point (4,1) undergoes the following three successive transformations ,
reflection about the line y=x−1
translation through a distance 1 unit along the positive direction
rotation thrpough an angle π4 about the origin in the anti - clockwise direction
Then the coordinates of the final point are ,
View SolutionA plane mirror is on y-z plane facing positive x-axis. A point object is present at (10,5). The mirror is translated by 2 units along positive x and 3 units along positive y-direction. Final image of the point object is at
View SolutionFind the co-ordinates of the point at at a distance 6 units from the point (1,1) in the direction making an angle of 60∘ with the positive direction of the x− axis.
View SolutionA circle of radius 2 units touches the co ordinate axes in the first quadrant. If the circle makes a complete rotation on the x-axis along the positive direction of the x-axis, then the equation of the circle in the new position is
View SolutionFind the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with positive direction of X axis is 15o.
View SolutionFind the position of the final image after three successive reflections taking the first reflection on m1 .
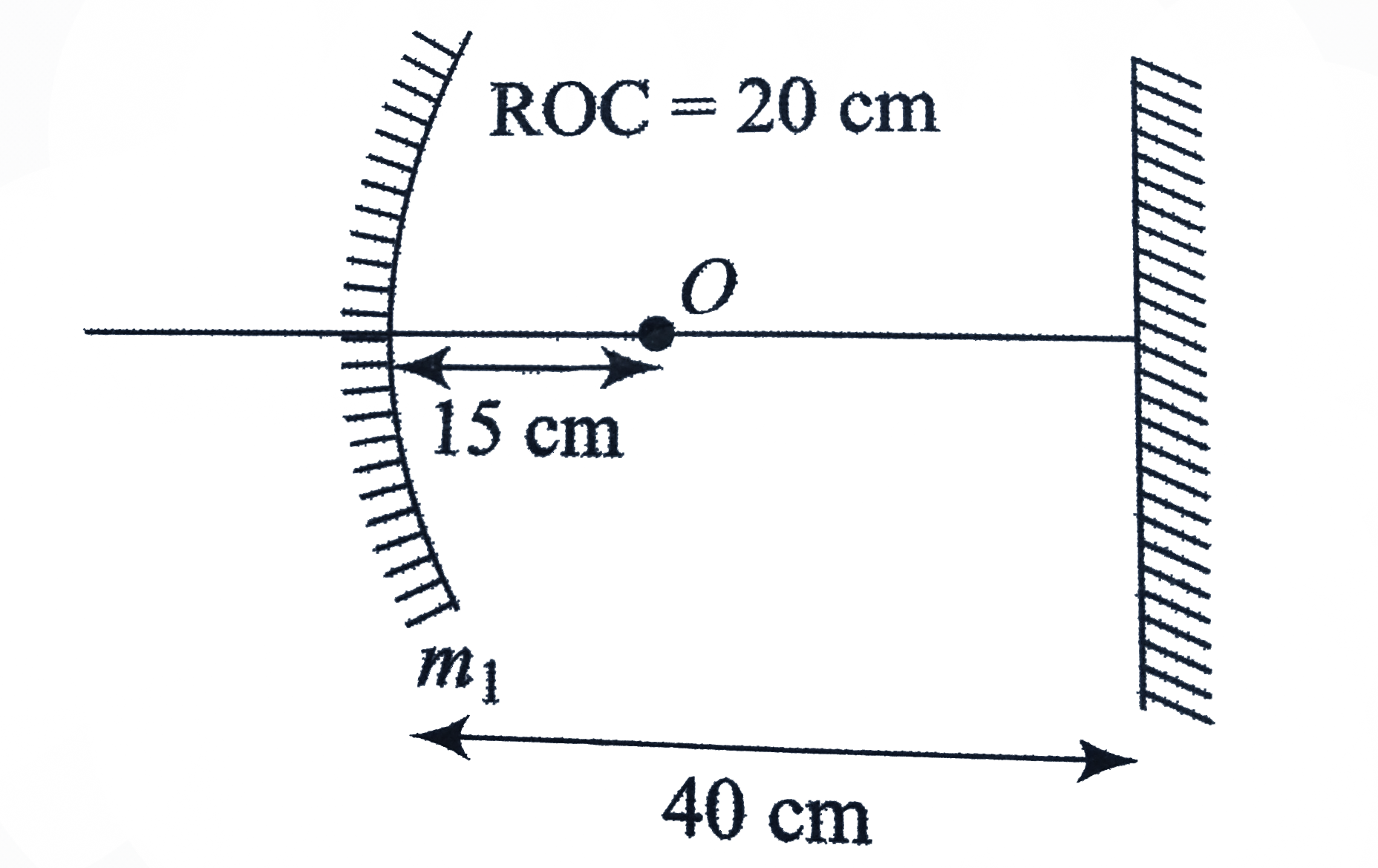
View SolutionThe point (4,1) undergoes the following two successive transformations
(i) Reflection about the line y=x
(ii) Translation through a distance 2 units along the positive X-axis.
Then the final coordinate of the point are
View Solution
