Find the probability distribution of the maximum of two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
To solve the problem of finding the probability distribution of the maximum of two scores obtained when a die is thrown twice, and to determine the mean of the distribution, we can follow these steps:
Step 1: Identify the Sample Space
When a die is thrown twice, the sample space consists of all possible pairs of outcomes. Each die has 6 faces, so the total number of outcomes when throwing a die twice is:
6×6=36
The sample space can be represented as:
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),…,(6,6)}
Step 2: Determine the Maximum Score
For each pair of outcomes, we need to find the maximum score. The maximum score X can take values from 1 to 6. We will count how many times each maximum score occurs.
- Maximum = 1: Only (1,1) → 1 outcome
- Maximum = 2: (1,2), (2,1), (2,2) → 3 outcomes
- Maximum = 3: (1,3), (2,3), (3,1), (3,2), (3,3) → 5 outcomes
- Maximum = 4: (1,4), (2,4), (3,4), (4,1), (4,2), (4,3), (4,4) → 7 outcomes
- Maximum = 5: (1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5) → 9 outcomes
- Maximum = 6: (1,6), (2,6), (3,6), (4,6), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) → 11 outcomes
Step 3: Construct the Probability Distribution Table
Now we can summarize the probabilities for each maximum score:
| Maximum (X) | Number of Outcomes | Probability P(X) |
|-------------|--------------------|-----------------------|
| 1 | 1 | 136 |
| 2 | 3 | 336=112 |
| 3 | 5 | 536 |
| 4 | 7 | 736 |
| 5 | 9 | 936=14 |
| 6 | 11 | 1136 |
Step 4: Calculate the Mean of the Distribution
To find the mean E(X), we use the formula:
E(X)=∑(Xi⋅P(Xi))
Calculating each term:
- For X=1: 1⋅136=136
- For X=2: 2⋅336=636
- For X=3: 3⋅536=1536
- For X=4: 4⋅736=2836
- For X=5: 5⋅936=4536
- For X=6: 6⋅1136=6636
Now summing these values:
E(X)=1+6+15+28+45+6636=16136
Final Result
The mean of the distribution is:
E(X)=16136
When a die is thrown twice, the sample space consists of all possible pairs of outcomes. Each die has 6 faces, so the total number of outcomes when throwing a die twice is:
6×6=36
The sample space can be represented as:
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),…,(6,6)}
For each pair of outcomes, we need to find the maximum score. The maximum score X can take values from 1 to 6. We will count how many times each maximum score occurs.
- Maximum = 2: (1,2), (2,1), (2,2) → 3 outcomes
- Maximum = 3: (1,3), (2,3), (3,1), (3,2), (3,3) → 5 outcomes
- Maximum = 4: (1,4), (2,4), (3,4), (4,1), (4,2), (4,3), (4,4) → 7 outcomes
- Maximum = 5: (1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5) → 9 outcomes
- Maximum = 6: (1,6), (2,6), (3,6), (4,6), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) → 11 outcomes
Now we can summarize the probabilities for each maximum score:
|-------------|--------------------|-----------------------|
| 1 | 1 | 136 |
| 2 | 3 | 336=112 |
| 3 | 5 | 536 |
| 4 | 7 | 736 |
| 5 | 9 | 936=14 |
| 6 | 11 | 1136 |
To find the mean E(X), we use the formula:
E(X)=∑(Xi⋅P(Xi))
Calculating each term:
- For X=1: 1⋅136=136
- For X=2: 2⋅336=636
- For X=3: 3⋅536=1536
- For X=4: 4⋅736=2836
- For X=5: 5⋅936=4536
- For X=6: 6⋅1136=6636
E(X)=1+6+15+28+45+6636=16136
The mean of the distribution is:
E(X)=16136
Topper's Solved these Questions
Similar Questions
Find the probability distribution of the number of sixes in three tosses of a die.
View SolutionObtain the mean of the following distribution.

View SolutionFind the probability distribution for number of heads obtained in two tosses of a coin.
View SolutionFind the mean of the following distribution :

View SolutionFind the mean of the following distribution:
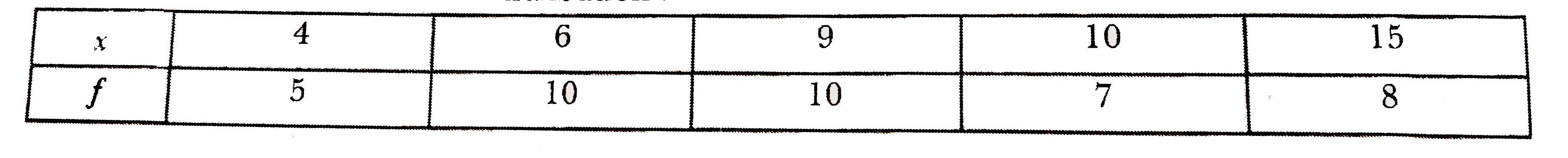
View SolutionFind the mean of the following distribution:

View SolutionFind the probability distribution for number of heads obtained in three tosses of a coin.
View SolutionFind the probability distribution of the number of heads when three coins are tossed.
View SolutionFind the probability distribution of the number of heads when three coins are tossed.
View SolutionFind the probability distribution of the number of doublets in four throws of a pair of dice. Also find the mean and variance of this distribution.
View Solution
