Find the ratio in which the area bounded by the curves $y^{2} = 12 x a n {d x}^{2} = 12 y$ is divided by the line $x = 3 .$

Video Solution

Text Solution

Verified by Experts

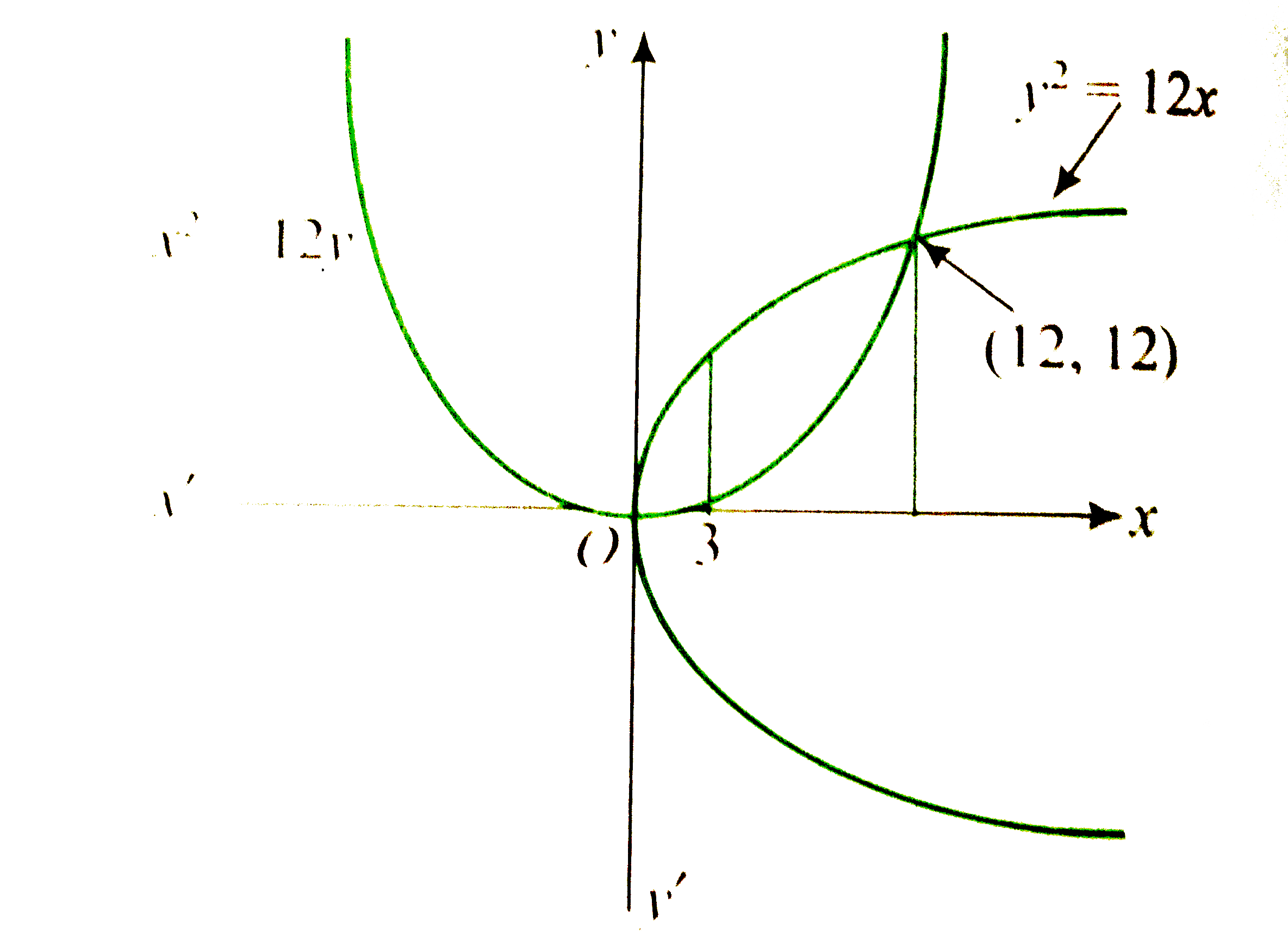
$A_{1} = Area bounded by y^{2} = 12 x, x^{2} = 12 y, and line x = 3$
$= \int_{0}^{3} \sqrt{12 x} d x \int_{0}^{3} \frac{x^{2}}{12} d x$
$= \sqrt{12} {∣ ∣ ∣ \frac{2 x^{3 / 2}}{3} ∣ ∣ ∣}_{0} - {∣ ∣ ∣ \frac{x^{3}}{36} ∣ ∣ ∣}_{0} = \frac{45}{4}$ sq. units
$A_{2} = Area bounded by y^{2} = 12 x and x^{2} = 12 y$
$= \frac{16 (3) (3)}{3} = 48$ sq. units
$∴ Required ratio = \frac{\frac{45}{4}}{48 - \frac{45}{4}} = \frac{45}{147}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area bounded by the curves $y^{2} = x^{3} and | y | = 2 x$ is
A $\frac{5}{16}$ sq units
B $\frac{16}{5}$ sq units
C $\frac{3}{8}$ sq units
DNone of these
The area bounded by the curve $y^{2} = 8 x$ and the line x=2 is
A $\frac{32}{3}$ sq. units
B $\frac{23}{3}$ sq. units
C $\frac{16}{3}$ sq. units
D $\frac{13}{2}$ sq. units

CENGAGE-AREA-Comprehension Type

Home
Ask Doubt
Profile